指数を含む関数の最大・最小

$a^x=t$ とおき、 $t$ についての $2$ 次関数の最大・最小について考えます。
$t$ の値の範囲が $t \gt 0$ であることに注意します。

例題１

関数 $y=2^x-4^x$ の最大値を求めなさい。

解説

定番パターンに対する慣れ、としか言いようがありません。

まずは、「底をそろえる」という基本からはじまります。
以下の解説のような式変形をします。

$y=2^x-4^x$
$=2^x-(2^2)^x$
$=2^x-(2^x)^2$

$2^x=t$ とおくと、$0 \lt t$
$y=t-t^2$

つまり、$2$ 次関数です。定義域が $0 \lt t$ での最大値を求めます。
$2$ 次関数の最大値を求めるのは数Ⅰで学習した通りになります。
つまり、グラフの概形を知ることで最大値を求めます。
これって平方完成をするということですね。

$y=t-t^2$
$=-(t-\displaystyle \frac{1}{2})^2+\displaystyle \frac{1}{4}$

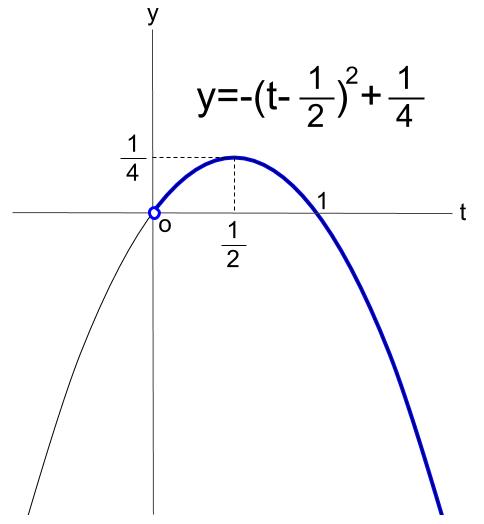
$0 \lt t$ の範囲でのグラフは上の青い太線部分です。
よって、$t=\displaystyle \frac{1}{2}$ で、最大値 $\displaystyle \frac{1}{4}$
をとります。

よって、$2^x=t$ とおいたので、 $t=\displaystyle \frac{1}{2}$ のとき、

$2^x=\displaystyle \frac{1}{2}$

$2^x=2^{-1}$
なので、
$x=-1$ で最大値 $\displaystyle \frac{1}{4}$ をとります。

例題2

$-1 \leqq x \leqq 3$ のとき、関数 $y=4^x-2^{x+2}$ の最大値と最小値を求めなさい。

解説

$2^x$ をもとに、 $2$ 次関数にできそうですね。
これは発想力ではなくて、例題 $1$ のように解く解法パターンを
知っているからこそです。

$y=4^x-2^{x+2}$
$=(2^2)^x-2^x×2^2$
$=2^{2x}-4×2^x$
$=(2^x)^2-4×2^x$

$2^x=t$ とおくと、
$y=t^2-4t$
である。

定義域は、
$-1 \leqq x \leqq 3$ より、$2^{-1 } \leqq 2^x \leqq 2^3$
なので、
$\displaystyle \frac{1}{2} \leqq t \leqq 8$

この範囲でのグラフをかきます。
$y=t^2-4t$
$y=(t-2)^2-4$
よって下図のようになります。

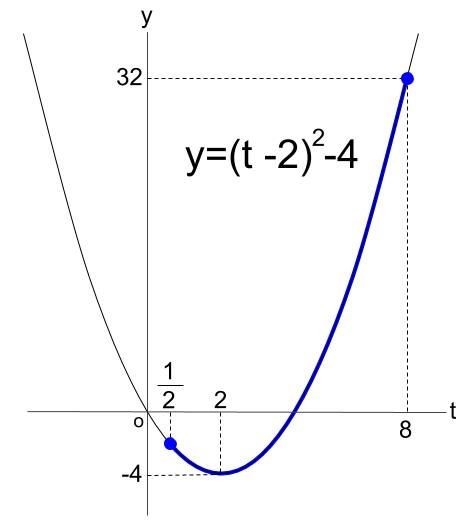
※グラフの比率は不正確です。わかりやすさ、かきやすさ優先でＯＫです。

よって、
$t=8$ のとき、つまり、 $2^x=8$ のときに最大値となる。
より、$x=3$ のとき、最大値 $32$
$t=2$ のとき、つまり、 $2^x=2$ のときに最小値となる。
より、$x=1$ のとき、最小値 $-4$