対数の定義

指数関数 \(y=a^x\) について、\(x\) を \(y\) で表すことを考えてみます。

簡単にいうと、指数とは逆向きのことを考えてみるのです。

指数とは逆の新しいもの、それが「対数」です。

例

例
指数関数 \(y=2^x\)

\(y=8\) のときの \(x\) を \(P\)
\(y=5\) のときの \(x\) を \(Q\)
とします。

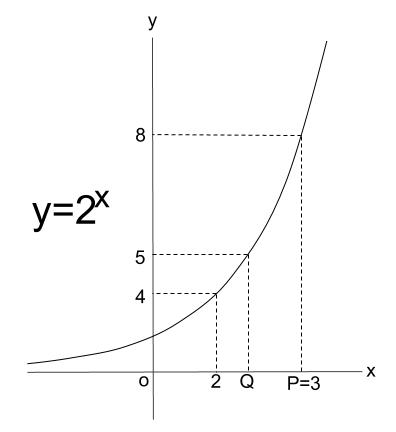
\(P=3\) は簡単に求まりますね。
\(8=2^P\) ということなので、\(P=3\) と求まります。

では
\(Q\) はいくつでしょうか。
\(5=2^Q\) ということですが、
\(Q\) はいくつなのでしょう？
計算をがんばれば、およそ \(Q=2.32\) 程度であることは求められます。
しかし数学においては、近似値ではなく、正確な値が欲しいのです。

実は、この \(Q\) の正確な値（近似値ではない値）は、
従来の関数やその組み合わせでは表現できないのです。
それならば、新しい記号をつくるしかありません。

\(5=2^Q\) を満たす \(Q\) は
\(Q=\log_{ 2 } 5\)
と表記します。

「ログ、２、５」と読みます。
\(2\) を底とする \(5\) の対数、とも読みます。
これこそが対数の定義です。

なにこれ？
意味わからない。
また難しそうなのが始まったな・・・

正直な感想で、結構です。

対数　ログは、慣れるまではわけわからない！
これは、誰でもそうなんです。
あたりまえです。

ただし、

ぜんぜん難しいこと、言っていませんよ！

新しい約束事が増えただけです。
暗記です。慣れです。
ただそれだけなので、難しいから嫌、というのは見当違いですよ。

中学 \(3\) 年生のときを思い出しましょう。
\(x^2=2\) を満たす正の数はおよそ \(1.41421356\) らしいのですが、
その値を正確に表記する方法がない。
ないので、根号という新しい記号を作りました。
\(\sqrt{2}\) は \(2\) 乗すると \(2\) になる数という決め事です。
そうです、ただの決め事です。

今回の対数も同じようなものです。
\(\log_{ 2 } 5\) という数値があるのです。
いくつだかわからないけど、周期のない小数です。

それで、これがどんな数なのかと言えば、 \(2^x=5\) の
\(x\) の値であると。

\(a^{\log_{ a } b}=b\)
ということです。

ただそれだけです。ただの決め事です。

指数と対数

\(a \gt 0\) 、\(a \neq 1\) で　 \(b \gt 0\) のとき
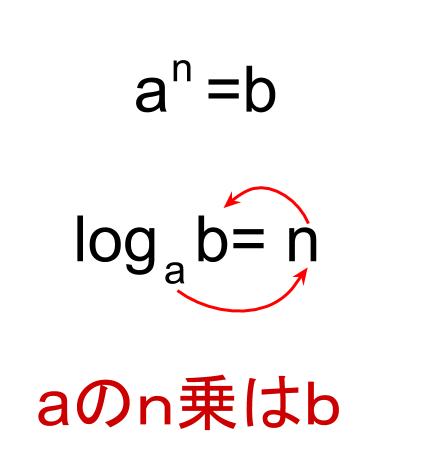
\(a^n=b\)
と
\(\log_{ a } b=n\)
は同じことを示してます。
指数と対数は同じことを示しています。
表現が違うだけです。

どちらも \(a\) の \(n\) 乗が \(b\) であることを示しています。
対数（ログ）も、同じように読んでしまうのがおススメです。
読む順序を覚えましょう。

\(\log_{ a } b=n\)　の \(a\) を底、 \(b\) を真数といいます。
底は指数のときから継続されてたものですね。
新しくでてきたのが真数です。
真数、底、ともに \(0\) より大きいです。
ここはしっかり覚えておきたいところです。

例題１

次の式を、\(\log_{ a } b=n\) の形で表しなさい。

\(16=4^2\)

解説

\(\log_{ 4 } 16=2\)

覚えるしかありませんが、「何乗なのか」が対数です。

例題２

次の式を、\(a^n=b\) の形で表しなさい。

\(3=\log_{ 2 } 8\)

解説

覚えるしかありませんよ。
この式の左辺は、\(3\) 乗だ！と言っているのです。
何の \(3\) 乗が何なのか、

\(2^3=8\)
です。

例題３

次の値を求めなさい。
（１）\(\log_{ 4 } 64\)

（２）\(\log_{ 3 } \displaystyle \frac{1}{81} \)

（３）\(\log_{\frac{1}{2} } 8\)

（４）\(\log_{ 2 } 1\)

解説

これはつまり、対数を用いないでスッキリとした表記にしろ、という意味です。

スッキリとした表記になおせる対数なんてごく一部なのですが、
高校生にテストで出題されるのは、このごく一部のものたちなわけです。

\(\sqrt{16}\) はいくつ？と聞かれれば

\(\sqrt{16}=4\) ですね。
ほとんどの \(\sqrt{n}\) は無理数ですけど、ごく一部のものは整数になります。
その、整数になるものだけが問題として出題されるわけです。
対数の基本計算問題もこれと同じようなものです。

解説（１）\(\log_{ 4 } 64\)

\(\log_{ 4 } 64\) は、\(64\) は \(4\) の何乗か、という意味です。

\(4^3=64\) ですから、

\(\log_{ 4 } 64=3\)
です。

解説（２）\(\log_{ 3 } \displaystyle \frac{1}{81} \)

\(\log_{ 3 } \displaystyle \frac{1}{81} \)

\( \displaystyle \frac{1}{81} = \displaystyle \frac{1}{3^4}=3^{-4}\)

よって、
\(\log_{ 3 } \displaystyle \frac{1}{81} =-4\)

解説（３）\(\log_{\frac{1}{2} } 8\)

\(\log_{ \frac{1}{2} } 8\)

\(\log_{ \frac{1}{2} } 8=x\) とおけば、

\((\displaystyle \frac{1}{2})^x=8\)

\((2^{-1})^x=2^3\)

\(2^{-x}=2^3\)
よって、
\(-x=3\)
\(x=-3\)

（４）\(\log_{ 2 } 1\)

\(\log_{ 2 } 1\)

あらゆる数が \(0\) 乗すると \(1\) になります。
指数の基本法則です。

よって、
\(\log_{ 2 } 1=0\)

※\(\log_{ a } 1=0\) ただし、\(a \gt 0\)
と公式化もできます。