和の記号 \(\varSigma\)（シグマ）による和の公式

今まで学習してきた数列の和の公式を、シグマを用いて表すと以下のようになります。

すべて今まで学習してきた公式ですよ。

全部覚えています！！と言えますか？

\(\varSigma\)（シグマ）にびびってしまって、頭の中が真っ白になっている人いませんか？
\(\varSigma\)（シグマ）なんてただの約束記号です。
ただの暗記ものです。

上の \(5\) つの式は、シグマという新しいルールから得られるものではありません。

今まで学習してきた「既知の式」を、シグマという表記で表し直しただけです。

つまり、改めてシグマを使って計算、証明したりすることではなく、
ただ公式として暗記するだけのものたちです。

例えば \(1\) つ目の式
\(\displaystyle \sum_{ k = 1 }^{ n } c=nc\)

なんて、
\(\underbrace{c+c+c+\cdots+c}_{ n個 }=nc\)

という式をシグマで表記しただけです。
\(k\) がどこにもなくて戸惑うかもしれませんが、結局は暗記です。
この記号はこれを表す、と覚えてください。

例題１

次の和を求めなさい。

（１）\(\displaystyle \sum_{ k = 1 }^{ 10 } k\)

（２）\(\displaystyle \sum_{ k = 1 }^{ 12 } k^2\)

（３）\(\displaystyle \sum_{ k = 1 }^{ 10 } (-2)^k\)

（４）\(\displaystyle \sum_{ k = 1 }^{ n } 2^{k+1}\)

解答

（１）\(\displaystyle \sum_{ k = 1 }^{ 10 } k=1+2+3+\cdots+9+10\)

\(=\displaystyle \frac{1}{2}\cdot10(10+1)=55\)

（２）\(\displaystyle \sum_{ k = 1 }^{ 12 } k^2= 1^2+2^2+3^2+\cdots+11^2+12^2\)

\(=\displaystyle \frac{1}{6}\cdot12(12+1)(2\cdot12+1)=650\)

（３）\(\displaystyle \sum_{ k = 1 }^{ 10 } (-2)^k\)

\(=(-2)^1+(-2)^2+(-2)^3+\cdots+(-2)^{10}\)

\(=\displaystyle \frac{-2\{1-(-2)^{10}\}}{1-(-2)}\)

\(=682\)

（４）\(\displaystyle \sum_{ k = 1 }^{ n } 2^{k+1}\)

これは、ちょっと注意が必要です。

\(\displaystyle \sum_{ k = 1 }^{ n } 2^{k+1}=\displaystyle \frac{2(1-2^{n+1})}{1-2}\)

これだと間違っているのですけど、どこが間違っているかわかりますか？

まず、下の赤字部分が違います。

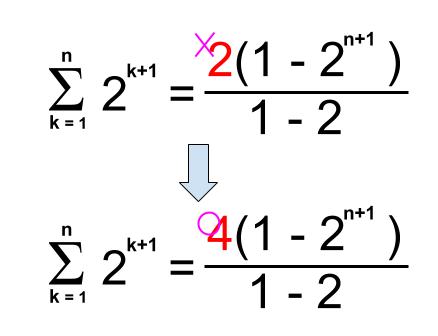
この赤字の箇所は、数列の初項でないといけません。
この数列の初項は、\(2^{1+1}=4\) ですね。

さらにあと \(1\) 箇所、間違いがあります。

下の赤字部分が違います。

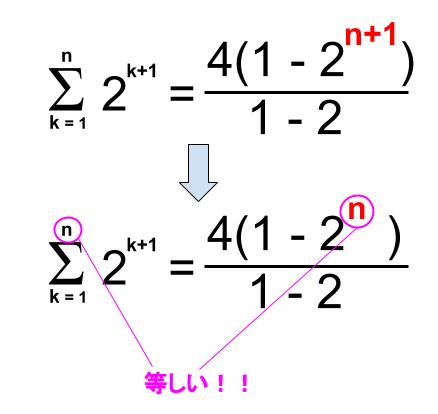
ここは、足し合わせる項の数が入る場所です。
ですから、\(2^{k+1}\) の指数の \(k+1\) につられてはいけません。

基本的なことですが、勘違いしやすい箇所です。気をつけましょう。

では改めて、正しく解きましょう。

\(\displaystyle \sum_{ k = 1 }^{ n } 2^{k+1}=\displaystyle \frac{4(1-2^n)}{1-2}\)

\(=4(2^n-1)\)

公式に慣れる、ただそれだけの問題です。
\(\varSigma\)（シグマ）にびびらないで下さいね。