三角形の辺、角の名前

ここからは、三角比を用いて、図形の性質を探っていきます。

三角形の辺の名前、角の名前は下の図のように表すこととします。

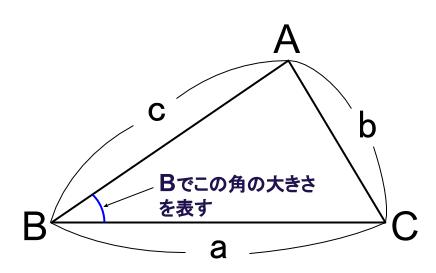
頂点の名前で、その内角の大きさを表します。
辺の名前は向かい合う角の小文字で表します。

簡略化した表示で、なかなか便利です。

正弦定理

正弦定理という、あらゆる三角形に成り立つ定理があります。

正弦定理
\(\triangle ABC\) の外接円の半径を \(R\) とすると

\(\displaystyle \frac{a}{\sin A}=\displaystyle \frac{b}{\sin B}=\displaystyle \frac{c}{\sin C}=2R\)

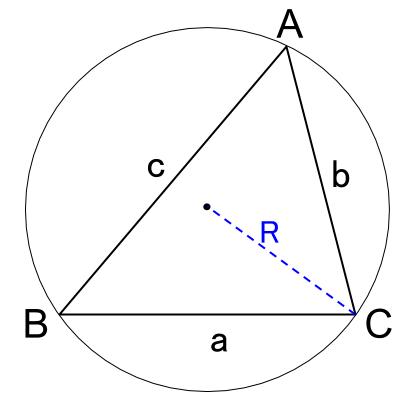
なぜこれが成り立つのか、は別ページに譲ります。
まずは、この定理をどのように用いるのか、例題で学習しましょう。

例題１

\(a=9,b=3\sqrt{6},A=120°\) のとき、\(B\) を求めよ。

解説

正弦定理は \(4\) つの項が、すべて等しいという等式でしたが、
問題を解くときに使うのは、そのうち \(2\) つの項です。

本問では、

\(\displaystyle \frac{a}{\sin A}=\displaystyle \frac{b}{\sin B}\)

ですね。
与えられた情報を入れると、

\(\displaystyle \frac{9}{\sin 120°}=\displaystyle \frac{3\sqrt{6}}{\sin B}\)

です。

\(\sin 120°=\displaystyle \frac{\sqrt{3}}{2}\) なので、

\(\sin B=\displaystyle \frac{1}{\sqrt{2}}\) と求まります。

これは、 \(B=45°,135°\) ですが、
\(A=120°\) ですから、
三角形の内角として適しているのは、\(45°\) の方です。
つまり、\(B=45°\) と求まります。

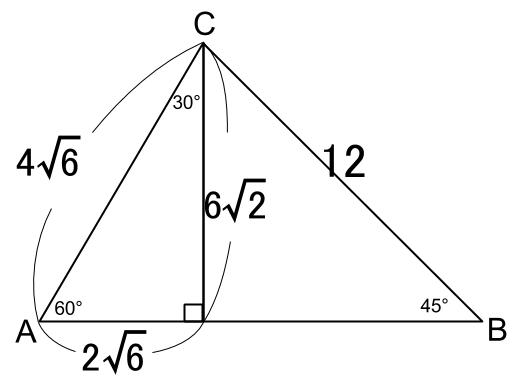
例題２

次のような三角形 \(ABC\) において、指定されたものを求めなさい。
\(a=12,A=60°,C=75°\) のとき、長さ \(b\)

解説

\(\sin 75°\) の値がわかりませんね。
この問題は、三角形の内角が \(2\) つ与えられているので、
\(B=45°\) がわかります。

よって、

\(\displaystyle \frac{a}{\sin A}=\displaystyle \frac{b}{\sin B}\)

を用います。

\(\displaystyle \frac{12}{\sin 60°}=\displaystyle \frac{b}{\sin 45°}\)

よって、
\(b=4\sqrt{6}\)
と求まります。

ちなみにこの問題は、三角形の内角がすべて与えらえているので、
三角形の形が \(1\) つに決まります。
さらに、三角形の内角のうち \(2\) つ以上が有名角の場合は、
図示をすることで容易に解決できます。

例題３

\(a=9\) 、外接円の半径\(R=9\) のとき、角 \(A\) を求めなさい。

解説

外接円の半径がでてきたら「正弦定理」です。
間違いありません。

\(\displaystyle \frac{a}{\sin A}=2R\)

を用います。

\(\displaystyle \frac{9}{\sin A}=2×9\)

よって
\(\sin A= \displaystyle \frac{1}{2}\)

より、\(A=30°,150°\)

本問では、どちらも答えとなります。

重要・自ら図示する

ちなみに、図形はどのようになっているのでしょうか？
「高校数学」においては、「機械的な計算処理」が求められることがほとんどで、図形的思考はなくともなんとかなる問題も多いです。

しかし、センター試験をはじめ、図形を自らかかないと解けない、解きにくい問題は出題されます。
ときには中学数学に戻って学習する心構えも持って、図形の学習に取り組みましょう。

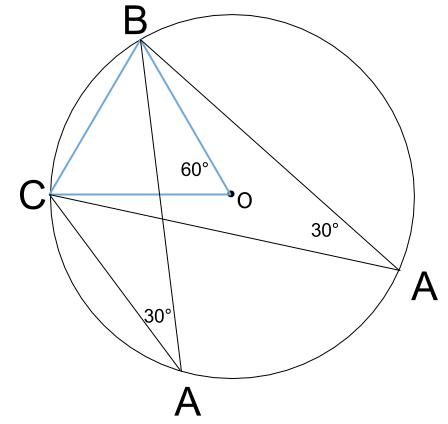
\(A=30°\) のとき

円周角が \(30°\) ならば、中心角は \(60°\) です。
つまり、三角形 \(OBC\) は正三角形です。
\(a=9\) 、外接円の半径\(R=9\) が成立していて、うまくいっていることが分かりますね。
点 \(A\) は弧 \(BC\) の長い方ならば、どこにあってもＯＫです。
つまり、あてはまる三角形は無限にあります。

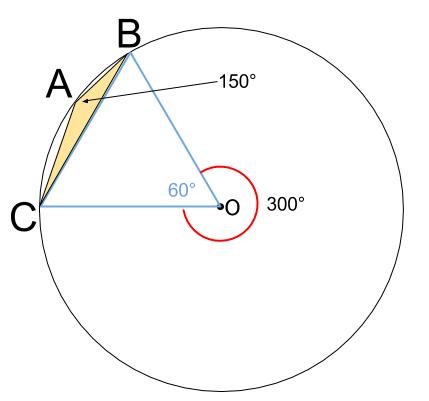
\(A=150°\) のとき

下図の小さい黄色い三角形 \(ABC\) のようになります。
円周角が \(150°\) ならば、中心角は \(300°\) です。
こちらの場合も、三角形 \(OBC\) は正三角形です。
\(a=9\) 、外接円の半径\(R=9\) が成立して、うまくっていることが分かりますね。
点 \(A\) は弧 \(BC\) の短い方ならば、どこにあってもＯＫです。
つまり、あてはまる三角形は無限にあります。

まとめ・正弦定理の使い方

つまり、

\(\displaystyle \frac{a}{\sin A}=\displaystyle \frac{b}{\sin B}\)

の \(4\) つの要素 \(a,b,A,B\) のうち、 \(3\) つが分かれば、最後の \(1\) つが求められます。

あるいは、

\(\displaystyle \frac{a}{\sin A}=2R\)
の \(3\) つの要素 \(a,A,R\) のうち、 \(2\) つが分かれば、最後の \(1\) つが求められます。

問題文に「外接円」と出てきたら「正弦定理」を使う。
もう条件反射しちゃってください。
「外接円」なんて他の分野ではまずでてきません。