三角関数の合成・その２

前ページに続いて、三角関数の合成についてです。

「三角関数の合成」とは加法定理の逆操作である。

この最大のポイントを覚えておいてください。
このページでも同様の話しかでてきません。

例題１

\(4\sin \theta -3\cos \theta\) を \(r\sin (\theta+ \alpha)\) の形で表しなさい。

解説

①\(r\sin (\theta+\alpha)=r\sin \theta \cos \alpha + r\cos \theta \sin \alpha \)
②\(r\sin (\theta+\alpha)=4\sin \theta -3 \cos \theta \)

①と②の係数を比較します。

①\(r\sin (\theta+\alpha)=\)\(r\)\(\sin \theta\)\( \cos \alpha\)\( +\)\( r\)\(\cos \theta\)\( \sin \alpha \)
②\(r\sin (\theta+\alpha)=\)\(4\)\(\sin \theta\) \(-3\)\( \cos \theta \)

\(r\cos \alpha=4\)
\(r\sin \alpha=-3\)
なので、以下のようになります。

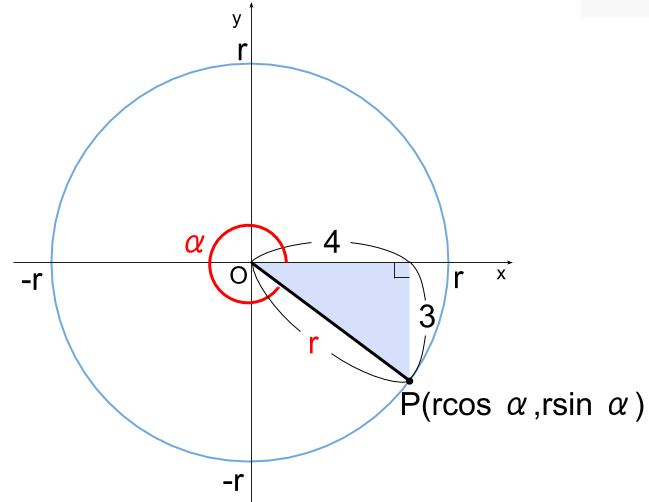
\(r=5\) は三平方の定理で求まりますが、
\(\alpha\) が何度なのかは求まりません。
三角関数の表を見れば、\(\alpha\) が \(323°\) と \(324°\) の間の角度であることはわかりますが、正確な角度は出せません。

このようなときは、\(\alpha\) は何度であるか求めてなくてＯＫです。
最終的な解答は以下のようにします。

\(4\sin \theta -3\cos \theta=5\sin (\theta+ \alpha)\)

ただし、\(\cos \alpha=\displaystyle \frac{4}{5}\)、\(r\sin \alpha=-\displaystyle \frac{3}{5}\)

このように、 \(\sin \alpha, \cos \alpha\) を書き添えることで、
\(\alpha\) は特定したことになります。

例題２

\(- \displaystyle \frac{1}{2}\sin \theta +\displaystyle \frac{\sqrt{3}}{2} \cos \theta\) を \(r\cos (\theta+ \alpha)\) の形で表しなさい。

解説

今まではずっと、\(r\sin (\theta+ \alpha)\) の形に合成してきました。
なんと今度は \(r\cos (\theta+ \alpha)\) の形にしろと。

大丈夫です。

とにかく、三角関数の合成は加法定理の逆と覚えておけばよいのです。

では、行きます。
コサインの加法定理の式です。これを用います。
\(\cos (\theta+\alpha)=\cos \theta \cos \alpha-\sin \theta \sin \alpha\)

①\(r\cos (\theta+\alpha)=r\cos \theta \cos \alpha-r\sin \theta \sin \alpha\)
②\(r\cos (\theta+ \alpha)=- \displaystyle \frac{1}{2}\sin \theta +\displaystyle \frac{\sqrt{3}}{2} \cos \theta\)

①と②の係数を比較します。

①\(r\cos (\theta+\alpha)=\)\(r\)\(\cos \theta\)\( \cos \alpha\)\(-\)\(r\)\(\sin \theta\)\( \sin \alpha\)
②\(r\cos (\theta+ \alpha)=\)\(-\)\( \displaystyle \frac{1}{2}\)\(\sin \theta +\)\(\displaystyle \frac{\sqrt{3}}{2}\)\( \cos \theta\)

つまり、

\(r\cos \alpha=\displaystyle \frac{\sqrt{3}}{2} \)

かつ

\(r\sin \alpha=\displaystyle \frac{1}{2}\)

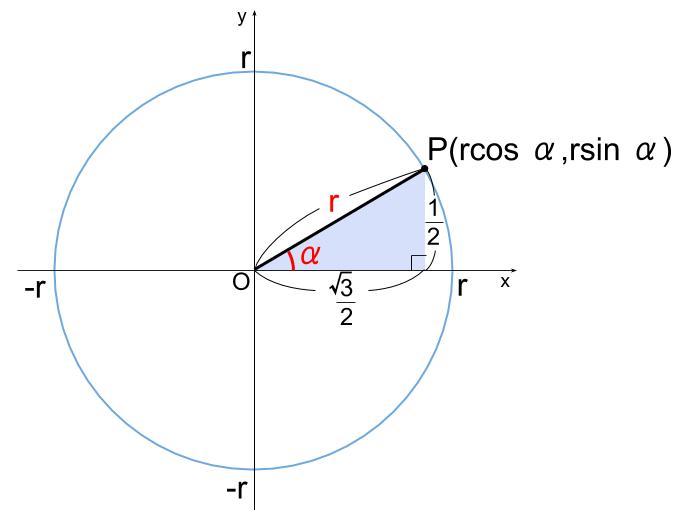
\(r=1\) と \(\alpha=30°\) と求まります。

よって、\(- \displaystyle \frac{1}{2}\sin \theta +\displaystyle \frac{\sqrt{3}}{2} \cos\theta =\cos (\theta+30°)\)

参考

この問題を、\(r\sin (\theta+ \alpha)\) の形に合成するとどうなるのか見ておきましょう。

答えを書いてしまいますが（自分で確かめてね！）

\(- \displaystyle \frac{1}{2}\sin \theta +\displaystyle \frac{\sqrt{3}}{2} =\sin (\theta+120°)\)

となります。

そもそも
\(\sin \theta= \cos (\theta-90°)\) なんですからね。
\(\sin (\theta+120°)=\cos(\theta+30°)\)
になるに決まっているのです！

\(\cos\) への合成、おそれるに足らずです！