そもそも三角関数の合成とは

三角関数の合成を練習してきました。

とにかく問題が解けるようになることが最大の関心事になりがちですから、
三角関数の合成の面白さ、不思議さに気づかないまま過ぎ去ってしまう人が多いのが実情です。

このページでは、そもそも三角関数の合成って何だろう？という点に焦点を当てます。

三角関数の合成をグラフで見てみよう

\(a \sin \theta + b \cos \theta =\sqrt{a^2+b^2} \sin ( \theta+ \alpha)\)

上の式は、
同じ角の 正弦と余弦を足し合わると、\(1\) つの正弦にできる
という意味です。

これをグラフで見てみましょう。
グラフで見てみれば、波（曲線）の重ねあわせです。

正弦の曲線と余弦の曲線を重ねあわせると、\(1\) つの正弦曲線になるのです。
不思議じゃないですか！

\(y=a \sin \theta\)

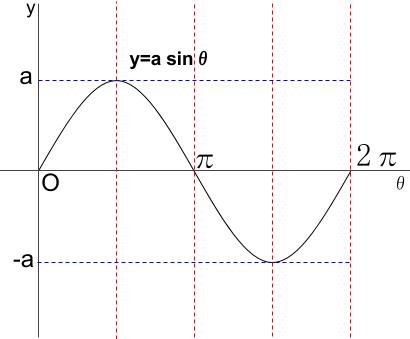
\(y=b \cos \theta\)

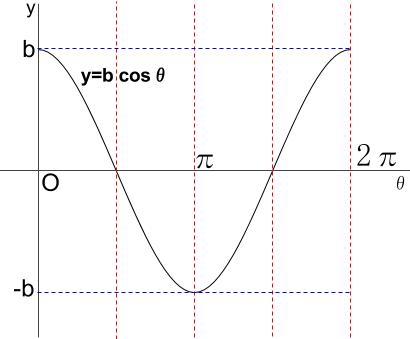
この \(2\) つの波を足します。
\(y=a \sin \theta + b \cos \theta\)
がどうなるのか見てみましょう。
\(\theta=0\) のとき、
\(a \sin \theta =0\)
\(b \cos \theta =b\)
なので、\(a \sin 0 + b \cos 0=b\)
となります。

これを\(0 \leqq \theta \leqq 2\pi\) の様々な \(\theta\) で行います。

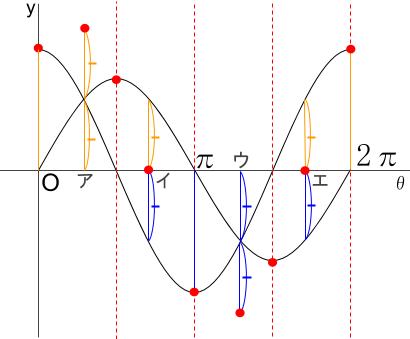
アやウでは、\(a \sin \theta =b \cos \theta \) なので、\(2\) 倍の位置に点をうちます。
イやエでは、\(a \sin \theta =-b \cos \theta \) なので、\(0\) に点をうちます。

無限個の点は打つ作業はやってられませんので、どうなるのか結果を見てしまいましょう。
\(y=a \sin \theta + b \cos \theta\) のグラフです。
なめらかな \(\sin\) カーブになります。

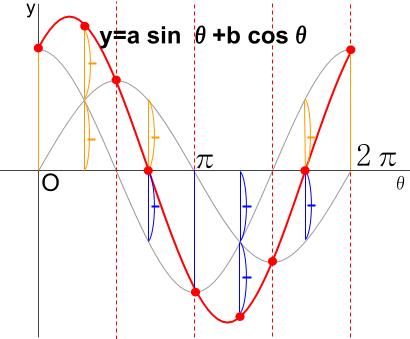
ちょうど良くきれいなサインカーブになるなんて、不思議じゃないですか！？

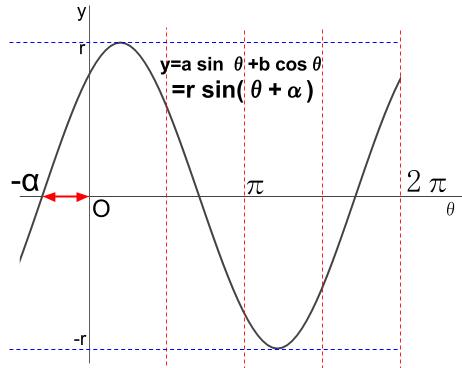
見ての通りですが、\(y=r \sin \theta \) を\(\theta\) 方向に平行移動したグラフになります。
平行移動分が、\(+ \alpha\) なわけです。

もちろんこの曲線は \(\cos\) であるという主張も正解なわけで、\(\cos\) への合成も可能なことがうなずけます。

周期が同じ \(2\) つの波を重ねると、同じ周期の \(1\) つの波になるのです。
※周期が異なる波を重ね合わせると、合成波は複雑なものになります。