三角関数の合成

↑ 何が何だかわかりませんね。
様々な参考書にある「三角関数の合成のまとめ」ですが、わかりにくいったらありません。
当サイトの究極の説明 ↓ を読んでいってくださいね。

三角関数の合成のポイント！

ずばり結論を書きましょう。
三角関数の合成と密接に関連しているのは

「加法定理」なのです。

もう一度合成の式に登場してもらいましょう

\(a \sin \theta + b \cos \theta =\sqrt{a^2+b^2} \sin ( \theta+ \alpha)\)

この式は、
「右辺を加法定理を用いてバラせば、左辺になる」
と解釈することができます。

もちろん我々がこれからやることは、その逆、
「左辺のバラバラの三角関数を合成して、右辺を作り出すこと」
です。

つまり、三角関数の合成とは、
加法定理の逆操作なのです！

まずこれを頭にたたきこみましょう。

例えるならば、
三角関数の展開が加法定理、合成は、三角関数の因数分解です。
もちろん因数分解の方が難しいわけです。

三角関数の合成を徹底分析する！

問題作成者はどうやってこの問題を作っているかというと、
答えを先に決めます。

ちなみにこの問題の答えは
\(2\sin (\theta+120°)\) です。
※度数法でいきます。弧度法の負荷は今はなしで、合成に集中しましょう。

これが答えになるように、先の問題を作っていきますよ。

\(2\sin (\theta+120°)\) を加法定理でバラバラにします。

\(2\sin (\theta+120°)=2\sin \theta \cos 120°+ 2\sin 120° \cos \theta\)

\(\cos 120°=-\displaystyle \frac{1}{2}\)

\(\sin 120° = \displaystyle \frac{\sqrt{3}}{2} \)

なので、

\(2\sin (\theta+120°)=2×(-\displaystyle \frac{1}{2}) \sin \theta + 2×( \displaystyle \frac{\sqrt{3}}{2}) \cos \theta\)

\(2\sin (\theta+120°)=-\sin \theta +\sqrt{3}\cos \theta\)

です。

これで問題ができました。

右辺のみを見せて、左辺の形に変形せよ、と出題するわけです。
\(r=2\) と \( \alpha =120°\) を求めろ、という問題なのです。

ですから、どうやって三角関数の合成をするのかというと
今見てきた流れを逆にたどるのです。

改めて問題として提示します。

では解いて行きますよ！
①\(r\sin (\theta+ \alpha)=r\sin \theta \cos \alpha+r\cos \theta \sin \alpha\)
②\(r\sin (\theta+ \alpha)=- \sin \theta +\sqrt{3} \cos \theta\)

①と②が等しくなるように係数を比較します。

①\(r\sin (\theta+ \alpha)=\)\(r\)\(\sin \theta\) \(\cos \alpha\)\(+\)\(r\)\(\cos \theta\)\( \sin \alpha\)
②\(r\sin (\theta+ \alpha)=\)\(-\)\( \sin \theta +\)\(\sqrt{3}\)\( \cos \theta\)

赤い部分に注目すれば、
\(r\cos \alpha =-1\)

青い部分に注目すれば、
\(r\sin \alpha = \sqrt{3}\)

これらを満たす \(r\) と \( \alpha \) を探せばいいわけです。

\(r\) と \( \alpha \) は、
半径 \(r\) の円周上から見つけます。

単位円ばっかり使ってきたのですが、
三角関数の合成においては半径 \(r\) の円を使う！
覚えちゃってください。
\(\cos \theta\) は \(x\) 座標
\(\sin \theta\) は \(y\) 座標
あたりまえですね！

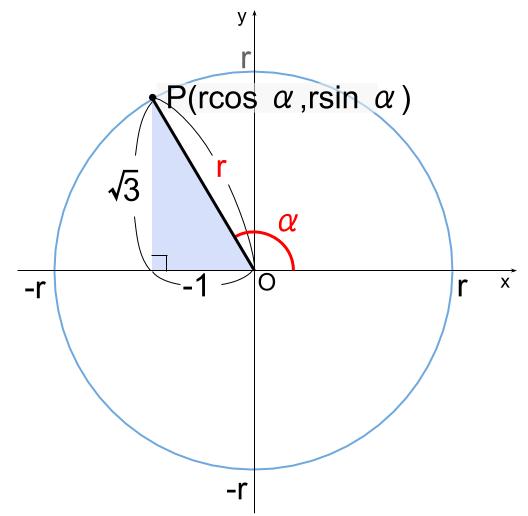
水色の直角三角形は、辺の比と角度を暗記している有名三角形ですね。
\(r=2\)
\( \alpha=120° \) と求まりました。
これで合成が完了したわけです！！
※ \(r\) は三平方の定理から求めても可。

つまり、
\(- \sin \theta +\sqrt{3} \cos \theta=2\sin (\theta+120°)\)

例題２

\(2 \sin \theta+ 2 \cos \theta\) を \(r\sin (\theta+ \alpha)\) の形で表しなさい。
ただし、\(0 \leqq \alpha \lt 2\pi\) とする。

解説

「合成は加法定理の逆」とまず暗記です。
加法定理の式と、係数の比較をします。

①\(r\sin (\theta+ \alpha)=r\sin \theta \cos \alpha+r\cos \theta \sin \alpha\)
②\(r\sin (\theta+ \alpha )=2 \sin \theta+ 2 \cos \theta\)

①\(r\sin (\theta+ \alpha)=\)\(r\)\(\sin \theta\) \(\cos \alpha\)\(+\)\(r\)\(\cos \theta\)\( \sin \alpha\)
②\(r\sin (\theta+ \alpha)=\)\(2\)\( \sin \theta +\)\(2\)\( \cos \theta\)

よって、
\(r\cos \alpha=2\)
\(r\sin \alpha=2\)

これを満たす \(r\) と \( \alpha \) は、
半径 \(r\) の円周上から見つけます。

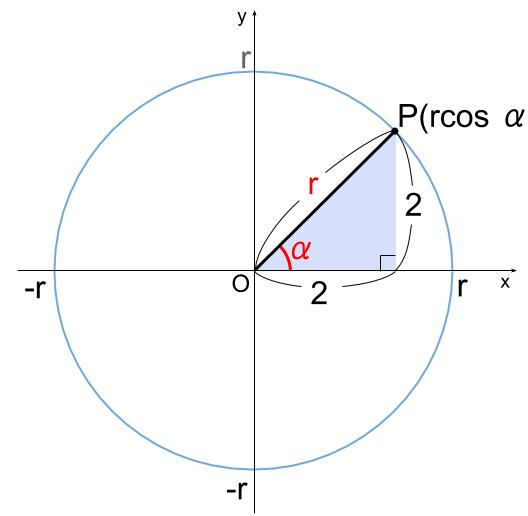
水色の直角三角形は、辺の比と角度を暗記している有名三角形ですね。
\(r=2\sqrt{2}\)
\( \alpha=45° \) と求まりました。

つまり、
\(2 \sin \theta +2 \cos \theta=2\sqrt{2}\sin (\theta+45°)\)