単位円の導入

直角三角形の辺の比から三角比を定義しました。
当然ですが、 \(\theta\) は鋭角の範囲に限られていました。

しかし・・・

\(100°\) とか \(250°\) とか、そんな角にも三角比を使えるようにしたい！
つまり、より広い範囲に適用できるようにしたい。
このように、三角比の拡張について考えます。

しかし・・・\(250°\) なんて三角形の内角には不可能です。
そんな拡張なんて無理な気がしますね。

この拡張のための突破口となるのが、斜辺の長さが \(1\) の直角三角形です。

角度とは回転である

斜辺の長さが \(1\) の直角三角形は無数にあります。
\(\theta\) の大きさによって無数にあります。

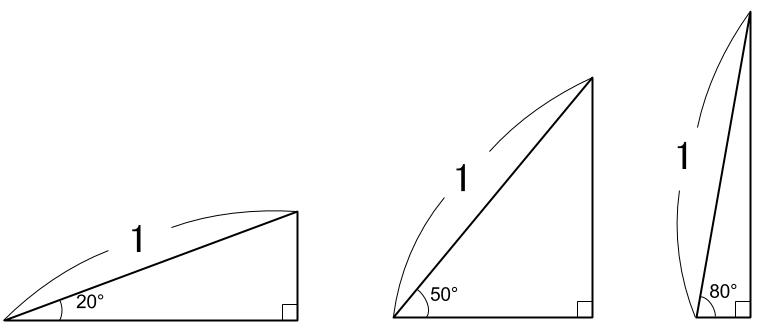
ここで

\(\theta\) の大きさを、どんどん大きくしていく

ということを考えます。
これって、つまり「回転」です。

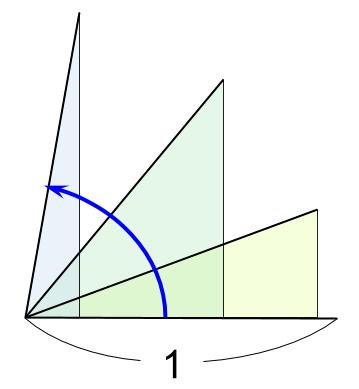
これって　長さ \(1\) の線分が回転しているようではないですか！！
三角比って、円と関係するんですね！！

回転の中心を座標平面の原点におくと・・・
おお！！座標と相性ばっちりです！！

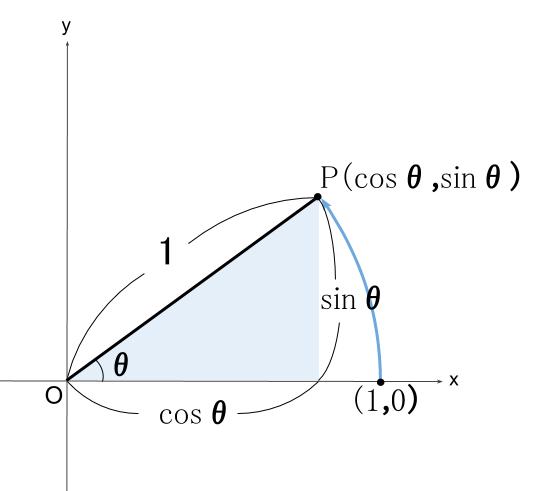
これこそが三角比の拡張版
単位円による三角比の定義です。
単位円とは、半径が \(1\) で、中心が原点の円のことです。

半径 \(1\) の線分 \(OP\) が、\((1,0)\) をスタート地点として、
反時計回りに \(\theta\) 回転したとき、
その線分の端、点 \(P\) が到達した地点の座標を \((\cos \theta , \sin \theta)\) とします。

この定義に従えば、「直角三角形の内角」にしばられることなく、\(\sin 120°\) や、\(\cos 150°\)を求めることができます。
つまり、\(90°\) を超えた角に対して、三角比を定義することができるわけです。

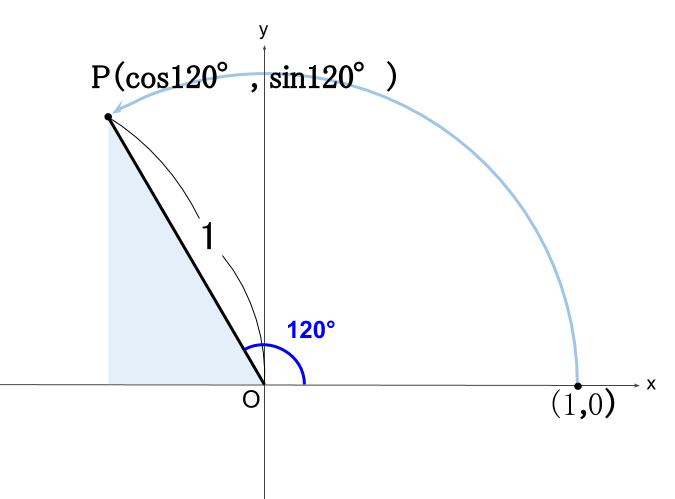
ちなみに、水色の直角三角形の辺の比から、点 \(P\) の座標が求まります。

点 \(P\) の \(x\) 座標 \(=\cos 120°=-\displaystyle \frac{1}{2}\)

点 \(P\) の \(y\) 座標 \(=\sin 120°=\displaystyle \frac{\sqrt{3}}{2}\)

もちろん、\(\tan 120°=\displaystyle \frac{y座標}{x座標}=-\sqrt{3}\)
となります。
\(1\) 次関数の傾きとまったく同じものです。
\(OP\) の傾きが \(\tan \theta\) です。

例題１

（１）\(135°\) の正弦、余弦、正接の値を求めなさい。

（２）\(150°\) の正弦、余弦、正接の値を求めなさい。

解説

で、結局出題されるのは有名角です。
\(30°,45°\) が関係する角のことです。
今まで通りに、三角定規の辺の比を用いて、三角比を求めます。

現カリキュラムでは、数学Ⅰにおいては、\(180°\) までの角を扱います。
数学Ⅱにおいて \(180°\) を超えた角まで扱います。
このページでは、 \(180°\) までの角を説明しますが、
\(180°\) を超えた角の三角比も上で説明した内容とかわりはありません。

（１）\(135°\) の正弦、余弦、正接の値

\(135°\) 回転した \(OP\) を単位円上にとります。
※作図は半円で十分ですね。

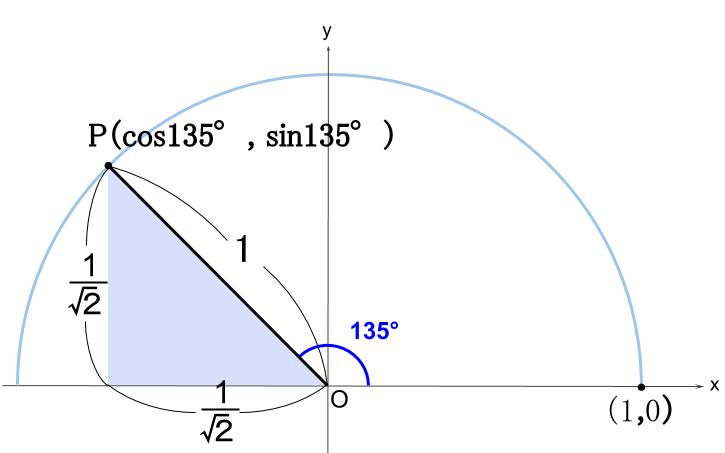
点 \(P\) の 座標は、直角三角形の辺の比からわかります。

点 \(P\) の \(x\) 座標 \(=\cos 135°=-\displaystyle \frac{1}{\sqrt{2}}\)・・・負ですよ！

点 \(P\) の \(y\) 座標 \(=\sin 135°=\displaystyle \frac{1}{\sqrt{2}}\)

このように、作図して求めます。
完全丸暗記をする必要はありません。

もちろん、\(\tan 135°=\displaystyle \frac{y座標}{x座標}=-1\)
となります。

（２）\(150°\) の正弦、余弦、正接の値

\(150°\) 回転した \(OP\) を単位円上にとります。
※作図は半円で十分ですね。

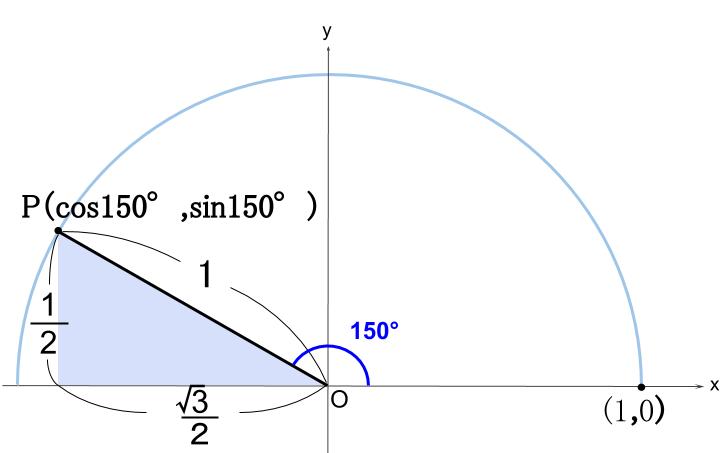
点 \(P\) の 座標は、直角三角形の辺の比からわかります。

点 \(P\) の \(x\) 座標 \(=\cos 150°=-\displaystyle \frac{\sqrt{3}}{2}\)・・・負ですよ！

点 \(P\) の \(y\) 座標 \(=\sin 150°=\displaystyle \frac{1}{2}\)

\(\tan 150°=\displaystyle \frac{y座標}{x座標}=-\displaystyle \frac{1}{\sqrt{3}}\)
となります。

以上、結局は有名角の三角比しか扱いません。
\(90°\) から \(180°\) の間の角としては、\(120°,135°,150°\) のみです。