\(90°- \theta,180°- \theta\) の三角比

以下のような公式？があります。

• \(\sin \theta=\cos (90°- \theta)\)
• \(\cos \theta=\sin (90°- \theta)\)
• \(\tan \theta=\displaystyle \frac{1}{\tan (90°- \theta)}\)
• \(\sin \theta=\sin (180°- \theta)\)
• \(\cos \theta=-\cos (180°- \theta)\)
• \(\tan \theta=-\tan (180°- \theta)\)

まったく暗記する必要はありませんし、
むしろ暗記してはいけません。
－（マイナス）がつくかどうか間違えないように完璧に暗記するなど、無意味な労力です。

直角三角形を図示すれば、すぐに導かれることばかりです。

どのように、直角三角形の図示から解答が導かれるのか。
この解法・利用法の流れを覚えて、自分で再現できるかを練習することが大事です。

例題１

\(\sin 65°\) を \(45°\) 以下の角の三角比で表しなさい。

解説

図示します。
合同な直角三角形を回転、裏返しをするだけです。

\(\sin 65°=b=\cos 25°\)
がすぐにわかりますね！

よって、\(\cos 25°\) が答えとなります。

※ちなみにこれは \(\tan\) でも表せるのでしょうが・・・
これについては考える必要はありません。
厳密に言えば、それを考えなくてよいような問題文で出題すべきなんですけど。
あまり悩まないようにしてください。

例題２

\(\sin 130°\) を \(90°\) 以下の角の三角比で表しなさい。

解説

図示します。

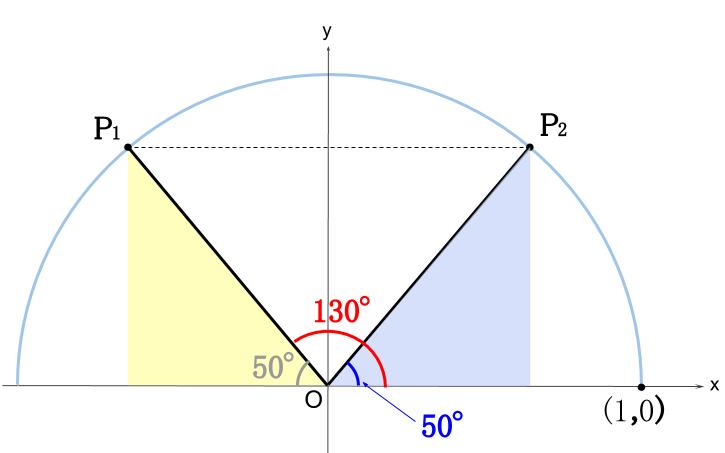
\(P_{1}\) の \(y\) 座標が \(\sin 130°\) ですから、
\(P_{2}\) の \(y\) 座標である \(\sin 50°\) と等しいですね。
つまり、\(\sin 130°=\sin 50°\) がすぐにわかりますね！

また、例題 \(1\) のような、合同な直角三角形の図示をすることで、
\(\sin 50°=\cos 40°\)　もわかります。

よって、\(\sin 50°,\cos 40°\) の \(2\) 通りが答えです。

例題３

\(\tan 70°\) を \(45°\) 以下の角の三角比で表しなさい。

解説

図示します。

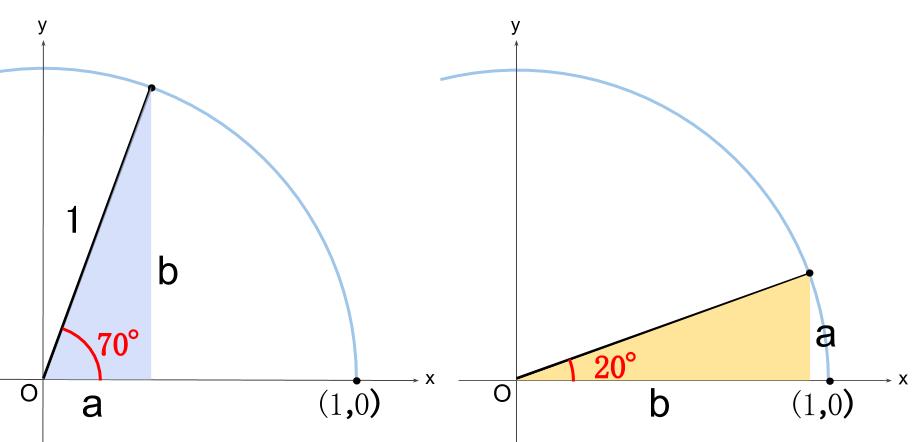
\(\tan 70°=\displaystyle \frac{b}{a}\)

これをどうやって、 \(45°\) 以下の角の三角比にするか。
これはもう下の解法を暗記しましょう。

\(\tan 20°=\displaystyle \frac{a}{b}\)

なので、
\(\tan 20°\) の逆数が \(\tan 70°\) です。
つまり、
\(\tan 70°=\displaystyle \frac{1}{\tan 20°}\)

これが答えです。

例題４

次の三角比を、鋭角の三角比で表しなさい。
① \(\cos 160°\)
② \(\tan 160°\)

解説

上と同様に、単位円と直角三角形の図示により答えを導きます。
①
\(\cos 160°=-\cos 20°\)
\(-\cos 20°=-\sin 70°\)

よって答えは、 \(-\cos 20°,-\sin 70°\) となります。

②
\(\tan 160°\) は負の値です。
しかし、鋭角の \(\tan\) は正の値です。
よって、答えには \(-\) がつきますね。
\(\tan 160°=-\tan 20°\)

\(-\tan 20°=-\displaystyle \frac{1}{\tan 70°}\)

よって答えは、\(-\tan 20°,-\displaystyle \frac{1}{\tan 70°}\) となります。