三角比をふくむ式から角度を求める

今までは、「\(\sin 30°\) を求めよ」のように、角度が与えられて、その三角比を求めてきました。

このページでは、逆向きのことを考えます。

つまり、三角比の値から、角度を求めます。

もちろん、「有名角」しか出題されません。
結局は有名角なんです。

例題

\(0° \leqq \theta \leqq 180°\) のとき、次のような \(\theta\) を求めなさい。

\(\sin \theta =\displaystyle \frac{\sqrt{3}}{2}\)

解説

「求める」もなにも・・・暗記しています・・・
\(\theta =60°\) です。

こんなことを思った人も多いことでしょう。

それでＯＫなんですけど、答えが複数あることを見落としてはいませんか？
「見落とさない」ためにも、
そして
「今後のより複雑な問題につなげる」ためにも、
単位円の図示をして解きましょう。
半径 \(1\) の円が単位円ですよ。

他の解き方もありますが、「単位円の図示」がもっとも学習効果の高い解法です。

\(0° \leqq \theta \leqq 180°\) の範囲なので、
半円をかきます。
単位円の半分です。

\(\sin \theta =\displaystyle \frac{\sqrt{3}}{2}\)とは、

\(y\) 座標が \(\displaystyle \frac{\sqrt{3}}{2}\) ということなので、

半円上で、\(y\) 座標が \(\displaystyle \frac{\sqrt{3}}{2}\) の点をとります。

\(2\) 点ありますね。

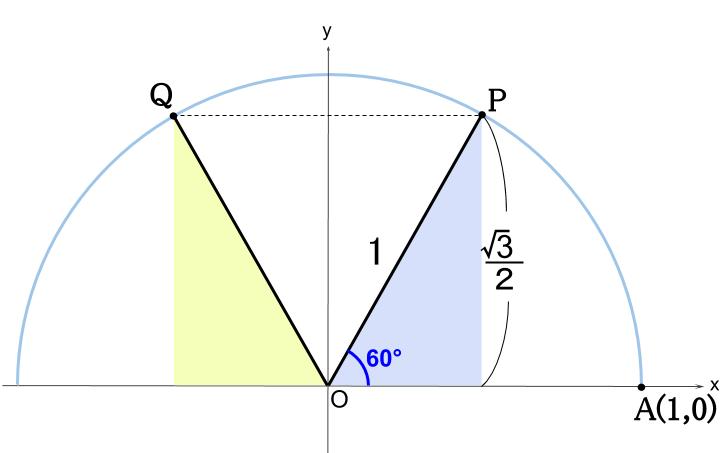
あとは、このときの角 \(AOP,AOQ\) を求めます。
有名角の辺の比は覚えていますね。

水色の直角三角形もクリーム色の直角三角形も、
\(30°,60°,90°\) の三角定規型です。

よって、
\(\theta=60°,120°\)
と求まります。

結局は、「三角定規型 \(2\) 種類の辺の比の暗記」がすべてです。
そして、それを「単位円でどのように用いるのか」という解法の暗記をしましょう。

例題２

\(0° \leqq \theta \leqq 180°\) のとき、次のような \(\theta\) を求めなさい。

\(\cos \theta =-\displaystyle \frac{1}{\sqrt{2}}\)

解説

図示です。

\(\cos \theta =-\displaystyle \frac{1}{\sqrt{2}}\)とは、

\(x\) 座標が \(-\displaystyle \frac{1}{\sqrt{2}}\) ということなので、

以下のようになります。

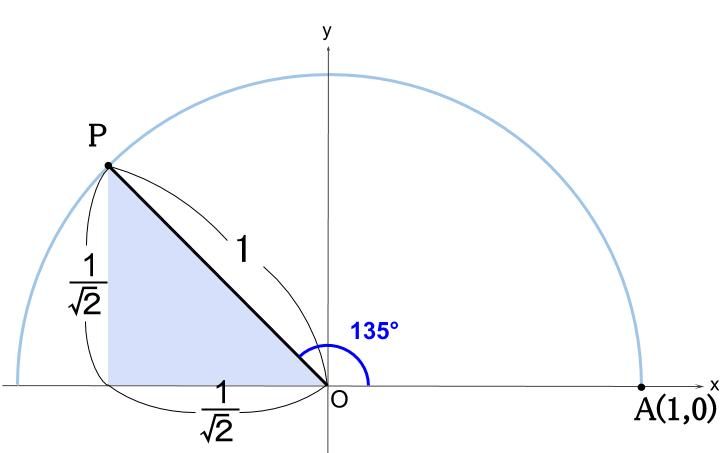
有名角の辺の比は覚えていますね。
水色の直角三角形は、
\(45°,45°,90°\) の三角定規型です。

\(\theta=135°\) と求まります。

例題３

\(0° \leqq \theta \leqq 180°\) のとき、次のような \(\theta\) を求めなさい。

\(\tan \theta =\displaystyle \frac{1}{\sqrt{3}}\)

解説

\(\tan\) は、直線の傾きなので、
単位円上の座標から求まるわけではありません。

まずは、有名三角形から探します。

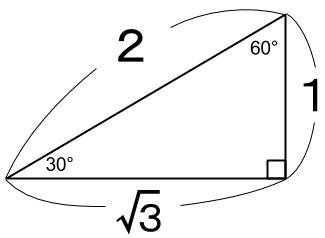
\(\tan \theta =\displaystyle \frac{1}{\sqrt{3}}\) は、
\(\theta=30°\)ですね。

これを単位円上でとってみれば、下図のようになります。
他に答えがないことがわかりますね。

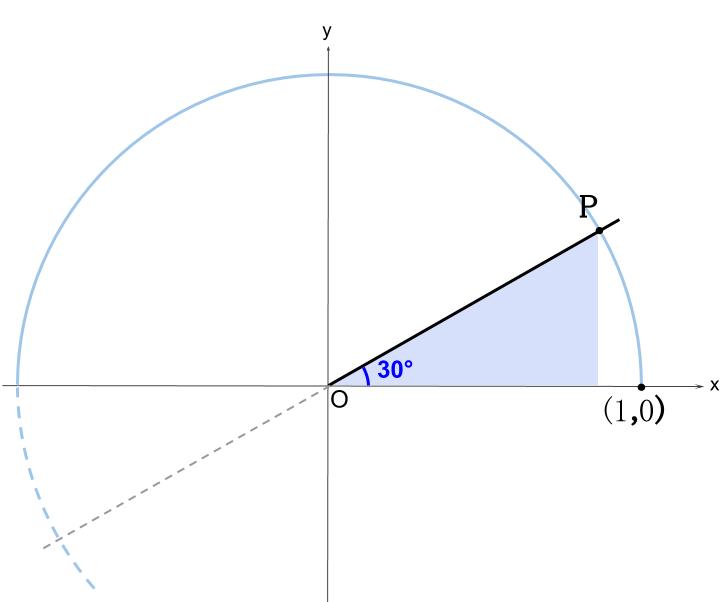
※\(0° \leqq \theta \leqq 180°\) の半円ではなく、
\(0° \leqq \theta \leqq 360°\) の円上でならば、
\(\tan 210° =\displaystyle \frac{1}{\sqrt{3}}\)
となり、複数の答えとなります。

例題４

\(0° \leqq \theta \leqq 180°\) のとき、次のような \(\theta\) を求めなさい。

\(\sin \theta =0\)

解説

\(y\) 座標が \(0\) ということなので、
\(0°\) と \(180°\) です。

参考

直角三角形にならない箇所ですが、\(0°,90°,180°\) もおさえておきましょう。
つまり、
三角定規型の有名角と、\(0°,90°,180°\) が大事です！

簡単ですよね。

\(\cos 90° =0\)

\(\cos 0° =1\)

\(\cos 180°=-1\)

\(\tan 0° =0\)

\(\tan 180° =0\)

単位円の図示で確認しておきましょう！