共通集合と和集合

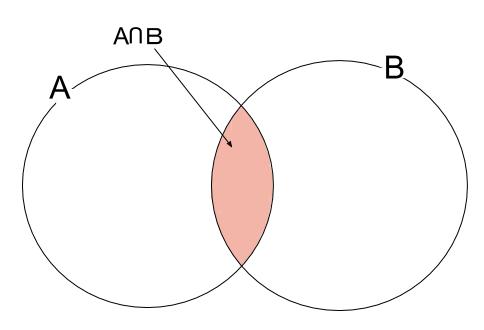
集合 $A,B$ の両方に入っている要素全体の集合を $A$ と $B$ の共通部分といい、
$A \cap B$
で表します。
$A$ かつ $B$ と読みます。

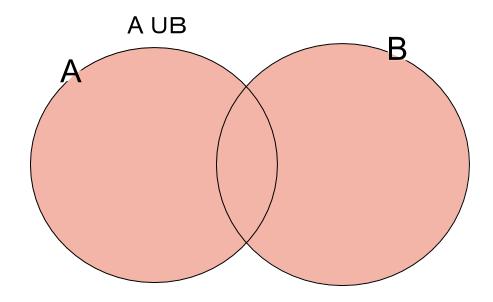
集合 $A,B$ の少なくとも一方に入っている要素全体の集合を $A$ と $B$ の和集合といい、
$A \cup B$
で表します。
$A$ または $B$ と読みます。

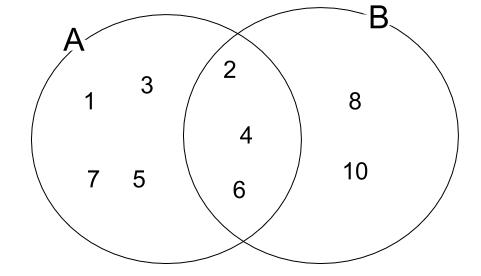
例
$Ａ=\{1,2,3,4,5,6,7\}$
$B=\{2,4,6,8,10\}$
のとき、
$A \cap B=\{2,4,6\}$
$A \cup B=\{1,2,3,4,5,6,7,8,10\}$

例2
$A=\{x | -2 \lt x \lt 3\}$
$B=\{x | 0 \lt x \lt 3\}$
のとき、$B \subset A$

補集合

全体集合 $U$ とその部分集合を $A$ とします。
$U$ の要素であって、 $A$ に属さない要素の集合を $\overline{ A }$ で表します。
これを $A$ の補集合といいます。
※ $\overline{ A }$ は $A$ バーと読みます。

例
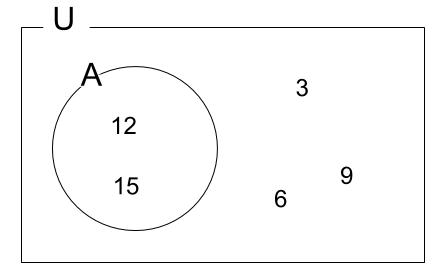
$U=\{3,6,9,12,15\}$
$A=\{12,15\}$
のとき、$\overline{ A }=3,6,9$

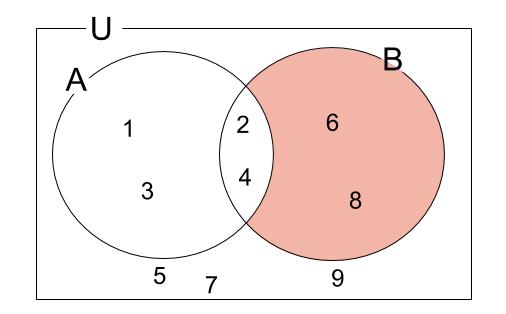
例題１

$U=\{1,2,3,4,5,6,7,8,9\}$ を全体集合とする。
$U$ の部分集合、$A=\{1,2,3,4\}$ 、$B=\{2,4,6,8\}$ について次の集合を求めなさい。
（１）$A \cap B$
（２）$A \cup B$
（３） $\overline{ A }$
（４） $\overline{ A } \cap B$

解説

ベン図による図示がおすすめです。
図を見ながら答えましょう。

（１）$A \cap B$
図より、$A \cap B=\{2,4\}$

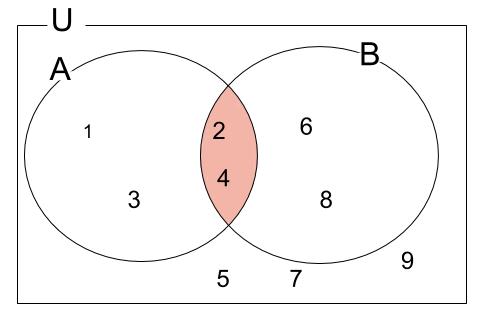
（２）$A \cup B$
$A \cup B=\{1,2,3,4,6,8,\}$

（３） $\overline{ A }$
$\overline{ A }=\{5,6,7,8,9\}$

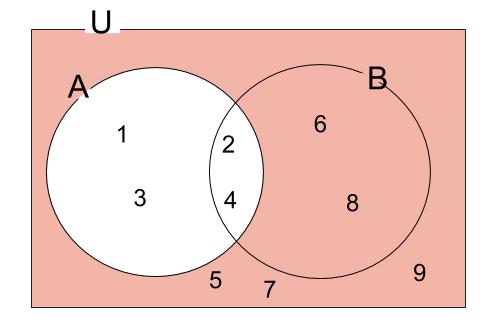
（４） $\overline{ A } \cap B$
$\overline{ A } \cap B=\{6,8\}$