記数法・\(10\) 進法から \(n\) 進法になおす

\(10\) 進法から \(n\) 進法

\(10\) 進法で表された数を \(n\) 進法で表すためには、機械的な計算方法があります。
しっかり理解をして使いこなしましょう。

例
\(10\) 進法で \(145\) を \(4\) 進法で表せ。

解答
以下のようにわり算をくりかえします（はしご算）。

\(145=2101_{(4)}\)
ということです。

深く考えずにこの手順で機械的に解けば良いのですが、この計算の意味についても理解しておきましょう。

これは「両替」とみなせば非常に理解しやすいでしょう。

細かいお金を、１段階ずつ両替していきます。
\(4\) 枚集まれない端数の \(1\) 円玉は、\(1\) 円玉のまま残ります。
\(4\) 枚集まれない端数の \(4\) 円玉は、\(4\) 円玉のまま残ります。
以下同様に続いていくのです。

例題

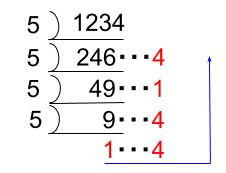
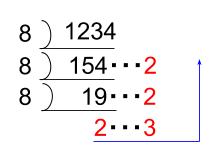
\(10\) 進法で表された \(1234\) を、\(5\) 進法、\(8\) 進法で表しなさい。

解答