センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

解説

座標が三角関数ですね。あまり見慣れない問題かもしれませんが、センター試験では良くある問題です。
ビビらないで普通に処理していきましょう！

\(OP=ア,PQ=イ\) ですが、ただの計算問題ですね。
\(OP=\sqrt{(2 \cos \theta)^2+(2\sin \theta)^2}=2\)

より、ア＝２

\(PQ=\sqrt{\{(2 \cos \theta +\cos 7\theta)-2 \cos \theta\}^2+\{ (2 \sin \theta +\sin 7\theta)-2\sin \theta\}^2}\)

\(=\sqrt{\cos^2 7\theta+\sin^2 7\theta}\)

\(=1\)

より、イ＝１

\(OQ^2\) もとにかく計算してみましょう。

\(OQ^2\)\(=(2 \cos \theta +\cos 7\theta)^2+( 2 \sin \theta +\sin 7\theta)^2\)

\(=4\cos^2 \theta+4\cos \theta \cos 7\theta+\cos^2 7\theta\)

\(+4\sin^2 \theta+4\sin \theta \sin 7\theta+\sin^2 7\theta\)

\(=4(\cos^2\theta+\sin^2\theta)+(\cos^2 7\theta+\sin^2 7\theta)\)

\(+4\cos \theta \cos 7\theta+4\sin \theta \sin 7\theta\)

\(=5+4(\cos \theta \cos 7\theta+\sin \theta \sin 7\theta)\)

ここまでは一直線ですね。

より、ウ＝５、エ＝４

次は、
\(5+4(\cos \theta \cos 7\theta+\sin \theta \sin 7\theta)\)\(=5+4\cos (オ\theta)\)
という変形を求められています。
※右辺は、ウ＝５、エ＝４を代入したもの

これは明らかに加法定理です。

\(\cos (オ\theta)=\cos \theta \cos 7\theta+\sin \theta \sin 7\theta\) です。

\(オ\theta=a\theta-b\theta\) とすれば、

\(\cos (a\theta-b\theta)=\cos a\theta \cos b\theta+\sin a\theta \sin b\theta\)
なので、
\(a=7,b=1\) が成り立ちます。

よって、\(オ＝a-b=6\)

オ＝６

当然ですが、
\(OQ^2=5+4\cos(6\theta)\)

がカギを握っています。

\(OQ\) は正なので、\(OQ\) が最大値のときに \(OQ^2\) が最大値をとり、かつ、\(OQ^2\) が最大値のときに \(OQ\) が最大値をとります。

よって、\(OQ^2=5+4\cos(6\theta)\) が最大値をとる \(\theta\) を求めます。

\(\displaystyle \frac{\pi}{8} \leqq \theta \leqq \displaystyle \frac{\pi}{4}\) の範囲なので、

\(6\) 倍して、

\(\displaystyle \frac{3}{4}\pi \leqq 6\theta \leqq \displaystyle \frac{3}{2}\pi\)

この範囲で \(\cos 6\theta\) は
\(-1 \leqq \cos 6\theta \leqq 0\) です。

よって、\(\cos 6\theta =0\) のときに、

\(OQ^2=5+4\cos(6\theta)=5\) という最大値をとります。

このとき、\( 6\theta =\displaystyle \frac{3}{2}\pi\) より、\( \theta =\displaystyle \frac{\pi}{4}\)

よりカ＝４

また、\(OQ^2=5+4\cos(6\theta)=5\) より、\(OQ \gt 0\) なので、\(OQ=\sqrt{5}\)

よりキ＝５

では後半戦です。

原点 \(O\) と\(P(2 \cos \theta ,2\sin \theta) \) を通る直線の方程式です。

中学生レベルの知識で解けばＯＫです。

直線の傾きは、\(\displaystyle \frac{2 \sin \theta}{2 \cos \theta}=\displaystyle \frac{\sin \theta}{\cos \theta}\)
※ \(\tan \theta\) ですけど、次の式変形があるので。

より、求める直線の方程式は、

\(y-2\sin \theta=\displaystyle \frac{\sin \theta}{\cos \theta}(x-2 \cos \theta)\)

整理すると、

選択肢３の\((\sin \theta)x-(\cos \theta)y=0\)

となります。
ク＝３

「このこと」とは直前に求めた直線 \(OP\) の方程式です。

つまり、点 \(Q\) が直線 \(OP\) 上にあれば良い、という条件から求められます。

\(Q(2 \cos \theta +\cos 7\theta, 2 \sin \theta +\sin 7\theta)\) を、\((\sin \theta)x-(\cos \theta)y=0\) に代入します。

\((\sin \theta)(2 \cos \theta +\cos 7\theta)\)\(-(\cos \theta)(2 \sin \theta +\sin 7\theta)=0\)

とにかく何か活路が見えるはずと信じて、計算を進めていきます。

\((2\sin \theta \cos \theta +\sin \theta\cos 7\theta)\)\(-(2 \sin \theta\cos \theta +\sin 7\theta\cos \theta)=0\)

これは・・・加法定理のときにでてくる項に似ていますから・・・
加法定理になるように変形します。

\((2\sin \theta \cos \theta -2 \sin \theta\cos\theta)\)\(+(\sin \theta\cos 7\theta-\sin 7\theta\cos \theta)=0\)

\(\sin \theta\cos 7\theta-\sin 7\theta\cos \theta=0\)

これは間違いなく加法定理ですね。

\(\sin(\alpha+\beta)=\sin \theta\cos 7\theta-\sin 7\theta\cos \theta\)

のはずですから、
\(\alpha= \theta\)
\(\beta=-7 \theta\)
でうまくいきます。

よって、\(\sin \theta\cos 7\theta-\sin 7\theta\cos \theta=0\) は、

\(\sin(\theta-7 \theta)=0\) と変形されます。

もちろん、\(\sin(-6\theta)=0\) です。

\(\displaystyle \frac{\pi}{8} \leqq \theta \leqq \displaystyle \frac{\pi}{4}\) の範囲でこれが成り立つのは、

\(\theta=\displaystyle \frac{\pi}{6}\)

より、ケ＝６

さて、最後です。

まず大事なことですが、（２）とは無関係な問題です。
（２）を長々と解いた後（３）ですから、（２）（３）が続きものであると勘違いが起きる可能性があります。

しかし。

（２）は\(3\) 点 \(O,P,Q\) が一直線上にあるような \( \theta\) の値を求めよう。

でした。

（３）は、\(\angle OQP\) が直角となるときです。

全く別のケースを考える問題です。（２）に引きづられないようにしましょう。

さて、解いていきましょう。

で・・・

何を使って解いたら良いのか・・・迷子・・・

こんな人、多そうです。

結論を言えば、

（１）を使うのです！

（１）と（３）は無関係ではありませんからね。

で、（１）を使うというヒントを読んで、自分で考えて解いてみてくださいね。

自力で解けましたか？

次も以外に盲点で、先に進めなくなってしまう人が多発しそうですが・・・

ずばり図示をしましょう！
基本ですね。

問題を解くために大事なことは情報整理です。
そして、情報整理の筆頭が図示ですね。

正確な情報はわかりませんが、図示をしてみるクセをつけましょう。

\(\angle OQP\) が直角とは、下図のようなとき

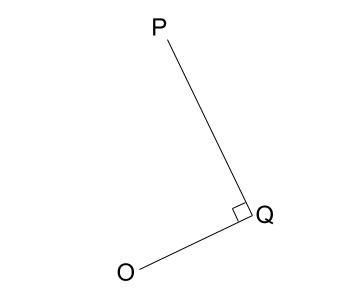
で、（１）でわかっていることって・・・

\(OP=2,PQ=1\) ですね。

あ！三平方の定理じゃないですか・・・

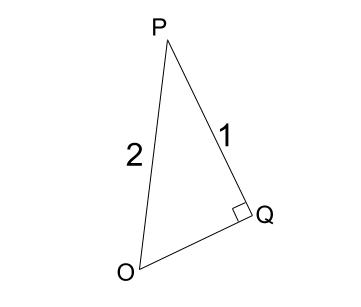
図の長さがおかしいですか、こんなこと、問題を解くときはよくあることです。

\(OQ^2=2^2-1^2=3\)
\(OQ\) は正なので、\(OQ=\sqrt{3}\)

より、コ＝３
※正しい図は、正三角形の半分、三角定規型でした。

（１）では、
\(OQ^2=5+4\cos(6\theta)\)
であることも求めました。

\(OQ=\sqrt{3}\) のとき

\(3=5+4\cos(6\theta)\)

\(\cos(6\theta)=-\displaystyle \frac{1}{2}\)

\(\displaystyle \frac{\pi}{8} \leqq \theta \leqq \displaystyle \frac{\pi}{4}\) の範囲で、これを満たすのは、

\(\theta=\displaystyle \frac{2}{9}\pi \)

より、サ＝２、シ＝９

以上、求まりました！