ko-su- センター試験ⅠA

【センター試験ⅠＡ】図形の性質02

センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

$\triangle ABC$ において $AB=2,AC=1,\angle A =90°$ とする。

$\angle A $ の二等分線と辺 $BC$ との交点を $D$ とすると、$BD=\displaystyle \frac{ア\sqrt{イ}}{ウ}$ である。

解説

これは、素早く正確に作図できる。もちろん不正確な作図でも答えを出せるのだけれど、
正確な作図の練習は常日頃からやっておくべきである。

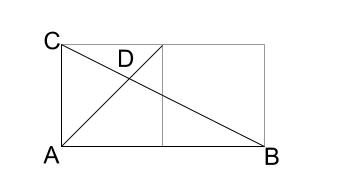
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その１$

まず正方形のマス目を薄くかいて、辺の長さの比 $2:1$ をとります。
目分量ではあるが、短時間で正確に近づけられるものはやっておきましょう。

角の二等分線と辺の比より、
$CD:BD=AC:AB=1:2$

つまり、$BD=BC×\displaystyle \frac{2}{1+2}$

$BC$ は三平方の定理より $\sqrt{5}$

よって、$BD=BC×\displaystyle \frac{2}{3}=\displaystyle \frac{2\sqrt{5}}{3}$

ア＝２、イ＝５、ウ＝３

では続きです。

点 $A$ を通り点 $D$ で辺 $BC$ に接する円と辺 $AB$ との交点で $A$ と異なるものを $E$ とすると、

$AB \cdot BE=\displaystyle \frac{エオ}{カ}$ であるから、 $BE=\displaystyle \frac{キク}{ケ}$ である。

解説

三角形が先にある状態から、円を作図するのはなかなか難しいものです。

あまりきれいにかけなくとも構いませんが、図形的性質を探ることで作図ができます。

下図のように、この円の中心 $O$ をとれます。

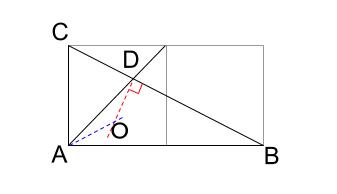
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その２$

まず、この円は点 $D$ で辺 $BC$ に接するので、赤い点線の上に中心があります。
そして、点 $A$ を通るので、$AO=DO$ です。目分量でとりましょう。
※$AD$ の垂直二等分線をとっても良いですね。

さて、フリーハンドでの円の作図ですから、歪んでもＯＫです。

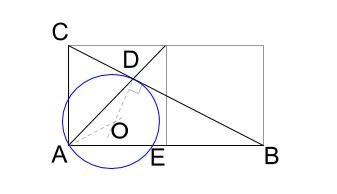
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その３$

さて、$AB \cdot BE$ を求めるのですが、これは図をみれば明らかに「方べきの定理」です。

$AB \cdot BE=BD^2$ で、$BD=\displaystyle \frac{2\sqrt{5}}{3}$ は先ほど求めていますから、

$AB \cdot BE=\displaystyle \frac{20}{9}$

より、エ＝２、オ＝０、カ＝９

また、$AB=2$ なので、

$2 \cdot BE=\displaystyle \frac{20}{9}$ より、

$BE=\displaystyle \frac{10}{9}$

より、キ＝１、ク＝０、ケ＝９

さて続きです。

次の $コ$ には下の０～２から、サには、３・４から当てはまるものを一つずつ選べ。

$\displaystyle \frac{BE}{BD} コ \displaystyle \frac{AB}{BC} $ であるから、直線 $AC$ と直線 $DE$ の交点は辺 $AC$ の端点 $サ$ の側の延長上にある。

０　$\lt$
１　$=$
２　$\gt$
３　$A$
４　$C$

解説

$サ$ は、図を正確にかいてきた人には、図を見ただけで検討がつきます。

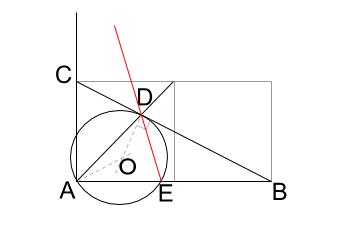
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その４$

$C$ の側で交わりますね。サ＝４です。

さてこれを論理的に説明するのが $\displaystyle \frac{BE}{BD} コ \displaystyle \frac{AB}{BC} $ の式になります。

特に頭を使わずに計算すれば、

$BE=\displaystyle \frac{10}{9}$

$BD=\displaystyle \frac{2\sqrt{5}}{3}$

$BC=\sqrt{5}$

は今まで求めてきました。$AB=2$ なので、

$\displaystyle \frac{BE}{BD} =BE÷BD=\displaystyle \frac{\sqrt{5}}{3} $

$\displaystyle \frac{AB}{BC} =\displaystyle \frac{2}{\sqrt{5}}=\displaystyle \frac{2\sqrt{5}}{5} $

よって、$\displaystyle \frac{BE}{BD} \lt \displaystyle \frac{AB}{BC} $

コ＝０　
です。

この不等式の意味するものは、下図のように平行になるとき、上の式は等号になるということです。

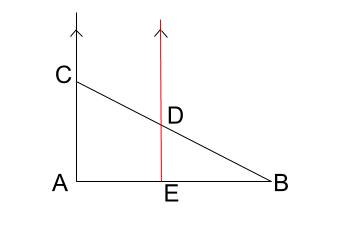
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その５$

では続きです。

直線 $AC$ と直線 $DE$ の交点を $F$ とすると、$\displaystyle \frac{CF}{AF} = \displaystyle \frac{シ}{ス} $ であるから、 $CF=\displaystyle \frac{セ}{ソ} $ である。

とにかく図である。

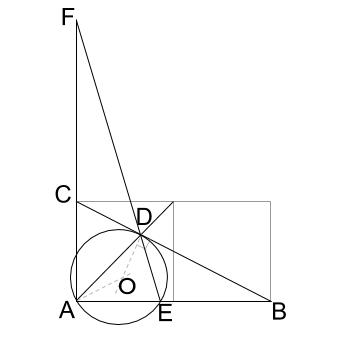
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その６$

$\displaystyle \frac{CF}{AF}$ を求めるのは、メネラウスの定理であるとすぐにわかりますね。

今までの図のままで解けるならそれで良いのですが、すでに図がごちゃごちゃになっている人は、ここで書き直すのもありです。

メネラウスを適用するためには、図は不正確で構わないので、

$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その７$

こんな図をさっと改めてかいてから計算するのも実践的です。
必要なのは、辺の比です。

$AB=2$、$BE=\displaystyle \frac{10}{9}$ なので、

$AE:EB=(2-\displaystyle \frac{10}{9}):\displaystyle \frac{10}{9}=4:5$

メネラウスの定理より、

$\displaystyle \frac{CF}{AF}=\displaystyle \frac{5}{8}$

※メネラウスの定理を使わずにこれを求める方法もおすすめで、このページにて解説しています。

メネラウスの定理・最終奥義

より、シ＝５、ス＝８

$AC=1$ なので、$CF=1×\displaystyle \frac{5}{8-5}=\displaystyle \frac{5}{3}$

より、セ＝５、ソ＝３

続きです。これで最後です。

したがって、$BF$ の長さが求まり、$\displaystyle \frac{CF}{AC} = \displaystyle \frac{BF}{AB} $ であることがわかる。
次のタには下の０～３から当てはまるものを一つ選べ。

点 $D$ は $\triangle ABF$ の　タ

０　外心である
１　内心である
２　重心である
３　外心、内心、重心のいずれでもない

解説

先のメネラウスの定理で、$AC:CF=3:5$ がわかった。
図に入れると

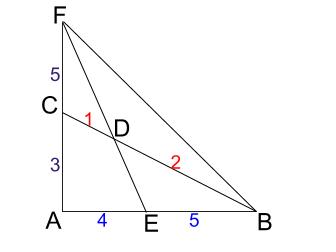
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その８$

問題文によれば、
「したがって、$BF$ の長さが求まり、$\displaystyle \frac{CF}{AC} = \displaystyle \frac{BF}{AB} $ であることがわかる」

本当に $BF$ の長さが求まるのか、そしてそれがいくつであるのかは一切聞かれていません。
その結果、$\displaystyle \frac{CF}{AC} = \displaystyle \frac{BF}{AB} $ である。

と教えてくれています。このことから $D$ が外心なのか内心なのか重心なのかが決まるよ
うです。

ではそこに注目すると、

$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その９$

これは、$BC$ が角 $B$ を二等分していることを示しています。

角の二等分線上に $D$ があるのですから、内心になりそうです。

こんなときは、先にかいていた正しい図や、問題分を読み返しましょう。
実際、角 $A$ の二等分線上に $D$ はあります。

タは　１です。

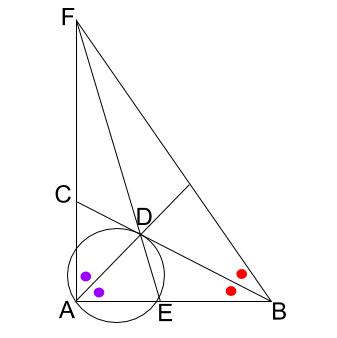
$高校数学無料学習サイトko-su- センター試験図形の性質本誌Ｈ30 その10$

※ $BF$ は三平方の定理で求まります。

カテゴリー: センター試験ⅠA