センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

解説

図示をまったくしないで答えることもできますが、感心しません。

まずは図示です。

視覚的に難度を下げて、ミスをしないように解きすすめていきましょう。

図は厳密に正確である必要はありませんが、可能な限り正しくかきます。

\(\cos \angle BAC =-\displaystyle \frac{\sqrt{3}}{3}\) から、

\(\angle BAC \) が鈍角であることが分かります。

ここからかきはじめましょう。\(CA=\sqrt{3}\) は約 \(1.73\) も知っていますね。

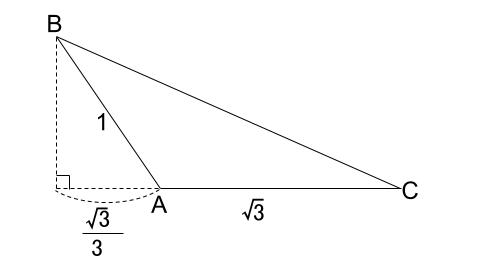
※不正確な図ですが、\(\angle BAC \) が鈍角であることなど、最低限を押さえてある図です。

余弦定理が使えることがすぐにわかりますね。\(\cos \angle BAC =-\displaystyle \frac{\sqrt{3}}{3}\) なので、

\(BC^2=1^2+(\sqrt{3})^2-2 \cdot 1 \cdot \sqrt{3} (-\displaystyle \frac{\sqrt{3}}{3})\)

\(BC \gt 0\) より、\(BC=\sqrt{6}\)、つまりア＝\(6\)

また、\(\triangle ABC\) は底辺 \(\sqrt{3}\)、高さ \(\displaystyle \frac{\sqrt{6}}{3}\) なので、

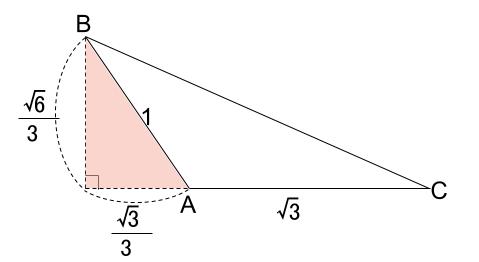
その面積は、\(\sqrt{3}×\displaystyle \frac{\sqrt{6}}{3}×\displaystyle \frac{1}{2}=\displaystyle \frac{\sqrt{2}}{2}\)

より、イ＝２、ウ＝２と求まります。

※高さの \(\displaystyle \frac{\sqrt{6}}{3}\) は、\(\sin^2 \theta +\cos^2 \theta =1\) から求めてもよいですし、左の薄い赤い直角三角形に三平方の定理を用いても良いです。

\(\sin \angle BAC=\displaystyle \frac{\sqrt{6}}{3}\) ですね。

では続きです。

解説

\(\triangle ABC\) の外接円をかきましょう。

\(\angle BAC \) の大きさが \(90°\) より大きいので、弧 \(BC\) は半円より長いことがわかります。
※円周角の定理ですが大丈夫ですか？分からない人は戻って \(1\) つずつ確認、暗記です。
姉妹サイト「中学数学学習サイトchu-cu-」

よって、おおよそ下図のようになります。

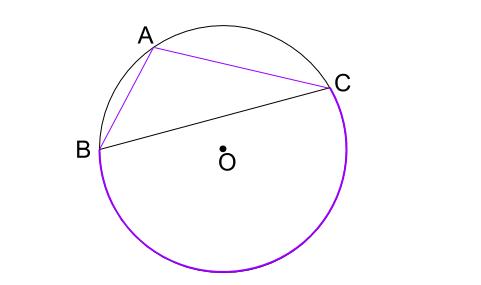
まず外接円からかいて、その後三角形をかいた方がかきやすいです。

はじめにかいた \(\triangle ABC\) とは別に、新しく作図するんですよ！！
こんなことを面倒だと思っていると、解けるようになりませんよ！

※\(\triangle ABC\) をはじめにかいた図とは反転させた図になっていますが、なんの問題もありません。そのときそのときで書きやすいように書くのです。

よって、\(D\) は下図のようになり、\(BD\) が外接円の直径であることも明らかです。
また、直径があれば、直角ですね。半円の弧の円周角は直角です。

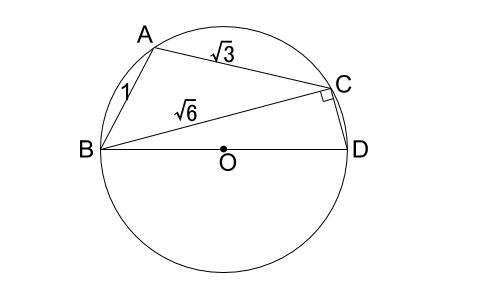
外接円とくれば、正弦定理に決まっています。
正弦定理より、

\(BD=\displaystyle \frac{\sqrt{6}}{\sin BAC}\)

\(\sin \angle BAC=\displaystyle \frac{\sqrt{6}}{3}\) は以前に求まっていますね。

計算すれば、\(BD=3\)　

よって、エ＝３です。

\(BD=3\) なので、\(\triangle BCD\) に三平方の定理を用いて \(CD=\sqrt{3}\)
\(\triangle BCD\) の面積は

\(\sqrt{6}×\sqrt{3}×\displaystyle \frac{1}{2}=\displaystyle \frac{3\sqrt{2}}{2}\)

より、オ＝３、カ＝２、キ＝２

では続きです。
あと空欄１か所です。

解説

\(CD=\sqrt{3},BD=3\) と、分かった情報は即座に図に入れます。
これらが次の問題を解くための鍵になることが非常に多いからです。

入れましたか？

即座に違和感を覚えるはずです。

\(AC=CD=\sqrt{3}\) と等しいのに、自分がかいた図は等しくないからです。

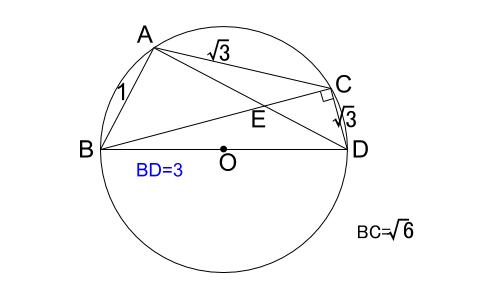
図が正確でなくとも、問題なく解けることもあります。
解けてしまう人はそれでＯＫです。

しかし、どうしても次の解き方が思いつかないとき、より正しい図を改めてかくことも一つの手なのです。

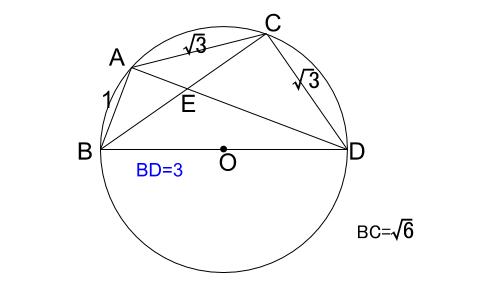
さて、ここからどうやって解くのか。
解法はたくさんあります。
どれが思いつくのか。人それぞれでしょう。

ここでは、最も簡潔に解ける解法を紹介します。
とりわけ、図をきちんとかいた人には思いつきやすいのではないでしょうか？

円周角が等しい！

　
弦 \(AC\) と弦 \(CD\) が等しいので、弧\(AC\) と弧 \(CD\) が等しくなっています。
つまり、\(2\) つの円周角が等しいのです。

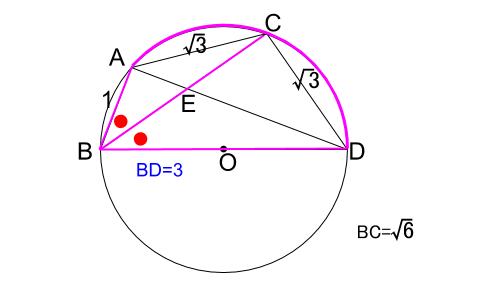
ここで、\(\triangle BDA\) に着目すると、
\(BE\) は角 \(B\) を \(2\) 等分しているため、

\(AE:DE=BA:BD=1:3\) です。

よって、\( \displaystyle \frac{AE}{DE}= \displaystyle \frac{1}{3}\)

ク＝１、ケ＝３

と求まりました。

参考

　
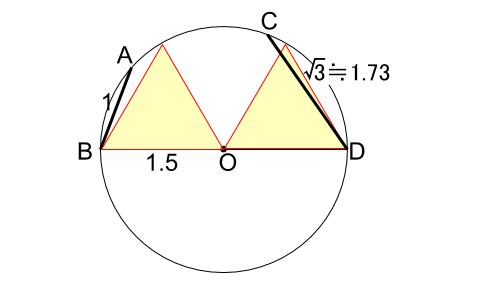
ちなみに、正三角形が下図のような配置なので、\(\sqrt{3}\) や \(1\) の長さが、正確に近くかけるのです。

\(1\) 辺が \(1.5\) の正三角形を基準にして、\(\sqrt{3}\) や \(1\) のおよその長さをかきます。