【センター試験ⅠA】図形の計量02
センター試験・過去問研究
センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう!
解説
正しい図はまだわかりませんが、簡単に図示します。

外接円の半径とくれば、正弦定理に決まっています。
外接円の半径を \(R\) とすると、正弦定理より、
\(2R=\displaystyle \frac{7\sqrt{3}}{\sin 60°}\)
より、\(R=7\)
ア=7です。
では、今後の問題にそなえて図示をしておきましょう。
\(\angle ACB =60°\) ですが、これは 弧 \(AB\) の円周角です。
つまり、弧 \(AB\) の中心角は \(120°\) です。
円と内接正六角形の図は絶対暗記の図です。
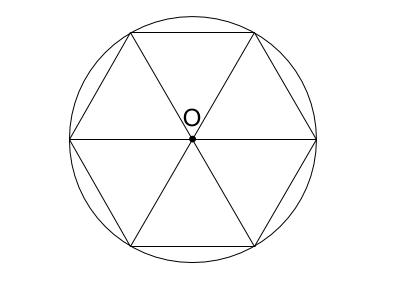
よって、弧 \(AB\) が決まります。
点 \(C\) はどこにあるのかは定まりませんが、弧 \(AB\) の長い方にあることは確かです。
円周角の定理そのものですね。点 \(C\) がどこにあっても、\(\angle ACB =60°\) とはこのことです。
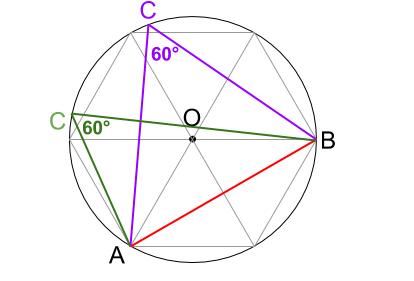
では続きです。
(1)\(2PA=3PB\) となるのは \(PA=イ\sqrt{ウエ}\) のときである。
点 \(C\) は弧 \(AB\) の長い方にあるので、
正確な図はわかりませんが、下図のようになりそうです。
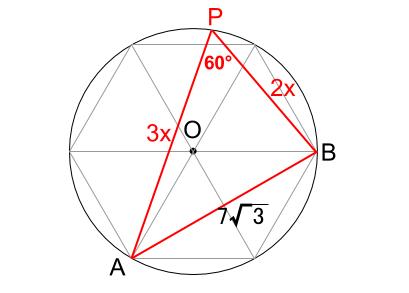
余弦定理により、
\((7\sqrt{3})^2=(3x)^2+(2x)^2-2\cdot 3x \cdot 2x \cdot \cos 60°\)
より、\(147=7x^2\)
\(x \gt 0\) より、\(x=\sqrt{21}\)
\(PA=3x=3\sqrt{21}\)
よって、イ=3、ウ=2、エ=1
(2)\(\triangle PAB\) の面積が最大となるのは \(PA=オ\sqrt{カ}\) のときである。
さまざまな \(P\) の位置を考えれば・・・
底辺 \(AB\) が固定されているので、高さが最も高くなるときです。
正三角形の内部構造まで考慮して作図していた人には、サービス問題です。
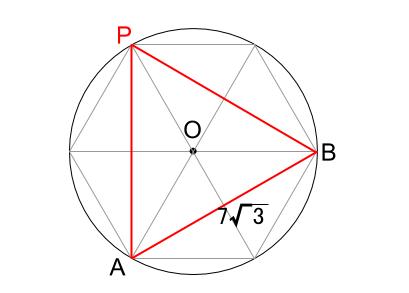
\(PAB\) は正三角形なので、\(PA=AB=7\sqrt{3}\)
より、オ=7、カ=3
(3)\(\sin \angle PBA\) の値が最大となるのは \(PA=キク\) のときであり、
このとき \(\triangle PAB\) の面積は \(\displaystyle \frac{ケコ\sqrt{サ}}{シ}\) である。
解説
\(\sin \angle PBA\) の値が最大なので、 \(\angle PBA=90°\) が可能かどうか、図で考えます。可能ですね。
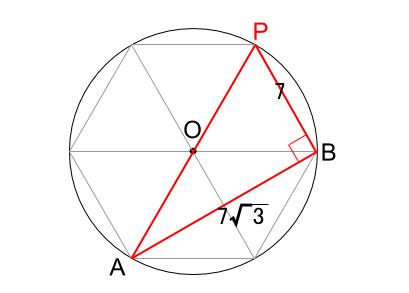
このとき、\(PA=14\)
半径 \(7\) の外接円の直径だからです。
より、キ=1、ク=4
また、\(\triangle PAB\) の面積は
\(7×7\sqrt{3}×\displaystyle \frac{1}{2}=\displaystyle \frac{49\sqrt{3}}{2}\)
より、ケ=4、コ=9、サ=3、シ=2
以上です。