1次不等式
1次不等式
不等式を学習します。
等式でなく、不等式です。
つまり、左辺と右辺が等しくないという式なのです。
「左辺が右辺より大きい」か「左辺が右辺より小さい」ことが示されているのが不等式です。
※普通 \(x \neq 3\) を不等式とはいいません。
不等号の意味、使用例
不等式では、不等号 \(\lt,\leqq,\gt,\geqq\) の \(4\) つの記号を用います。
その意味を、具体例を通じて見ていきましょう。
\( \lt \)
例
\( x \lt 2\)
この式の意味は、「\(x\) は \(2\) より小さい」です。「\(x\) は \(2\) 未満」ともいいます。
\(2\) は含まれないことが重要です。
数直線上での表現は以下のようになります。

含まない点は白丸、〇で表します。
\( \leqq \)
例
\( x \leqq 2\)
この式の意味は、「\(x\) は \(2\) 以下」です。\(2\) が含まれます。
つまり、\(x=2\) のケースもありなんです。
数直線上での表現は以下のようになります。

含む点は黒丸、●で表します。
\( \gt \)
例
\( x \gt -1\)
この式の意味は、「\(x\) は \(-1\) より大きい」です。「\(x\) は \(-1\) 超」ともいいますが、ほとんど使われない言い回しです。\(-1\) は含まれないことが重要です。
数直線上での表現は以下のようになります。

含まない点は白丸、〇で表します。
\( \geqq \)
例
\( x \geqq -1\)
この式の意味は、「\(x\) は \(-1\) 以上」です。\(-1\) が含まれます。
数直線上での表現は以下のようになります。

含む点は黒丸、●で表します。
不等式の性質
これはあたりまえですね。考えこむことなく使ってください。
3.\(a \lt b\) ならば、\(a-c \lt b-c\)
4.\(a \lt b\)、\(c \gt 0\) ならば、\(ac \lt bc\)、\(\displaystyle \frac{a}{c} \lt \displaystyle \frac{b}{c}\)
等式の性質とそっくり、と理解・暗記してください。
同じものを足したり引いたりかけたりしたとき、
大小関係が変わらないという意味ですから、あたりまえですよね。
最重要の性質がこちら↓です。
両辺に負の数をかけたり、両辺を負の数で割ったりすると、不等号の向きが変わります。
最重要です、しっかり暗記しましょう!
※なぜ不等号の向きが変わるのか。感覚的にわかりますよね。その程度の理解でOKです。
不等式を解く
\(x\) についての不等式があり、その不等式を満たす \(x\) の値を、不等式の解といいます。
不等式の解は \(1\) つではなく、無限にあることが普通です。
この解全体を求めることを、不等式を解くといいます。
具体例をどんどん見ていきましょう!
例題1
次の \(1\) 次不等式を解きなさい。
\(-5x-2 \lt x+4\)
解説
不等号が等号ならば、いわゆる \(1\) 次方程式です。
その \(1\) 次方程式を解くときと同様に、移項をします。
左辺が \(x\) の項、右辺が定数項になるようにします。
例題でやってみます。
\(-5x-2 \lt x+4\)
右辺の \(x\) を、左辺に移項して
\(-5x-x-2 \lt 4\)
\(-6x-2 \lt 4\)
左辺の \(-2\) を、右辺に移項して
\(-6x \lt 4+2\)
\(-6x \lt 6\)
ここで、 \(1\) 次不等式の解き方の最大のポイントです。
両辺を \(-6\) で割るわけですが、
負の数を両辺にかけると、不等号の向きが変わります。
負の数で両辺を割ると、不等号の向きが変わります。
先ほど、\(-6x \lt 6\) まで計算が進んでいましたね。
両辺を \(-6\) で割ると、
\(x \gt -1\)
このように、不等号の向きを変えます。
これだけが注意点です。
他の式変形は方程式を解くときまったく同じですね。
ちなみに、
\(x \gt -1\) が求める解全体です。
例題2
\(x+12 \leqq 6x-3\)
解説
\(x+12 \leqq 6x-3\)
\(x-6x \leqq -3-12\)
\(-5x \leqq -15\)
両辺を \(-5\) で割って、
\(x \geqq 3\)
これで求まりました。
不等号の下に等号があっても、なくても、
負の数で割ったら(かけたら)不等号の向きを逆にするのですよ!
例題3
次の不等式の解のうち、最大の整数を求めなさい。
\(\displaystyle \frac{3x+10}{2} \lt \displaystyle \frac{2-x}{3}\)
解説
両辺を \(6\) 倍して、分母をはらいましょう。
\(3(3x+10) \lt 2(2-x)\)
\(9x+30 \lt 4-2x\)
\(9x+2x \lt 4-30\)
\(11x \lt -26\)
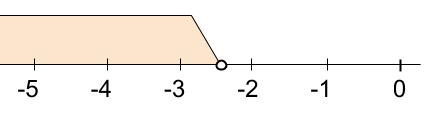
\(x \lt -\displaystyle \frac{26}{11}=-2\displaystyle \frac{4}{11}\)
よって、不等式の解のうち、最大の整数は、 \(-3\)