三角関数のグラフ

関数といえばグラフ！！

\(1\) 次関数、\(2\) 次関数・・・関数と言えばグラフで学習をしてきました。
今回もやります。
三角関数のグラフについて学習していきましょう！

\(y= \sin \theta\) のグラフ

でははじめに、\(y= \sin \theta\) のグラフから見ていきましょう。
※\(\theta\) は一般角です。　\(360°=2\pi\) を超えた角や、負の角も取ります。

グラフは以下のようになります。

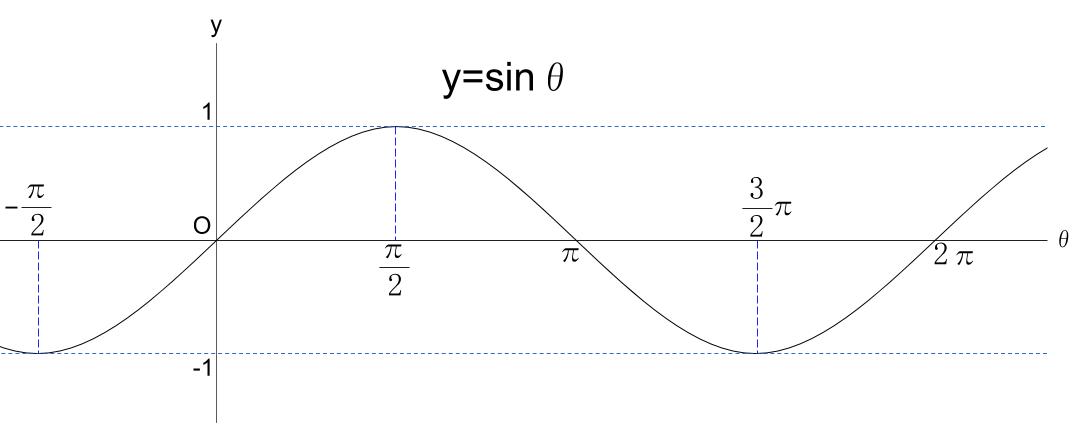
この曲線は、
\(\theta=0\) で \(y=0\)

\(\theta=\displaystyle \frac{\pi}{6}\) で \(y=\displaystyle \frac{1}{2}\)

\(\theta=\displaystyle \frac{\pi}{4}\) で \(y=\displaystyle \frac{\sqrt{2}}{2}\)

\(\theta=\displaystyle \frac{\pi}{3}\) で \(y=\displaystyle \frac{\sqrt{3}}{2}\)

\(\theta=\displaystyle \frac{\pi}{2}\) で \(y=1\)

このように、点を取っていくことで、グラフが完成します。

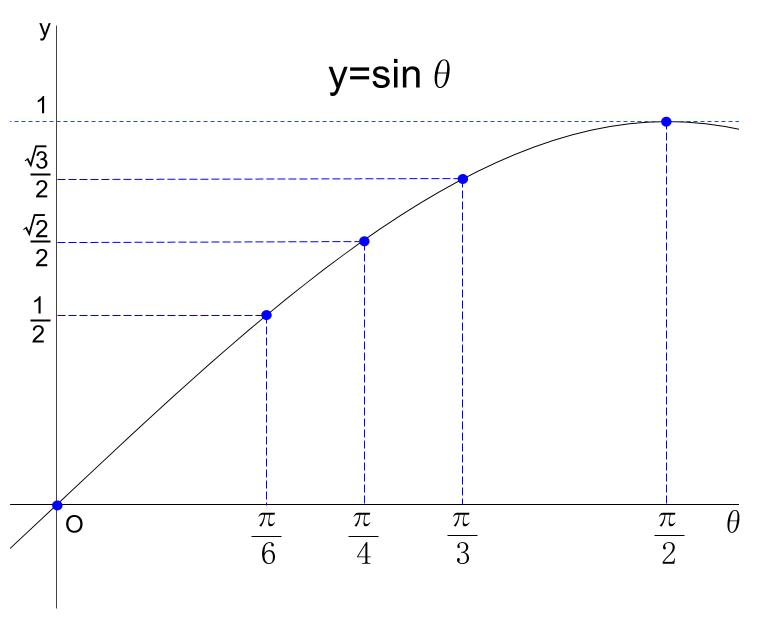
無限個の点をとる作業は無理なので、上のような曲線になるという事実を覚えてしまえばＯＫです。

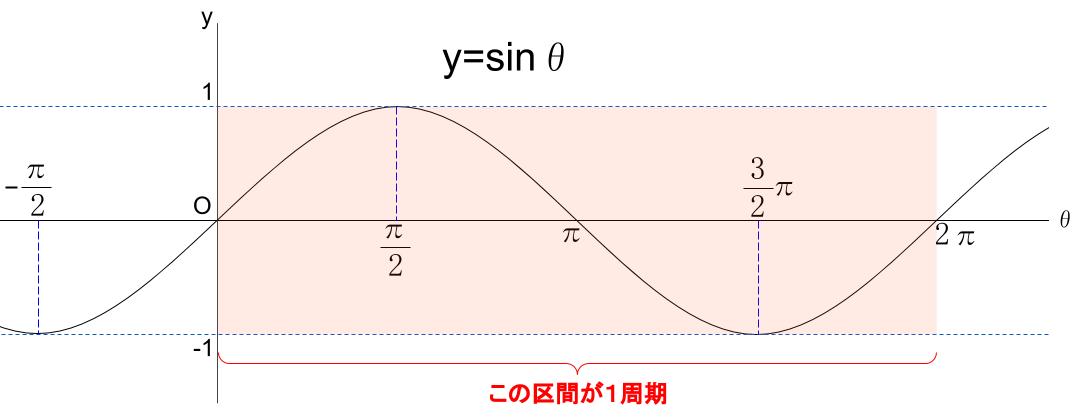
\(\theta\) が \(0\) から \(360°=2 \pi\) までで、円を \(1\) 周します。
その後は、同じ円をまた回るだけなので、
グラフは \(0\) から \(2\pi \) までのものを繰り返します。

これを周期としてあとはひたすら繰り返しです。
このことを周期が \(2\pi\) といいます。
関数の値域は \(-1 \leqq y \leqq 1\)

縮小して、広い範囲で見てみましょう。
\(-2\pi \leqq \theta \leqq 5\pi\)

\(y= \cos \theta\) のグラフ

同様にグラフをかくと以下のようになります。

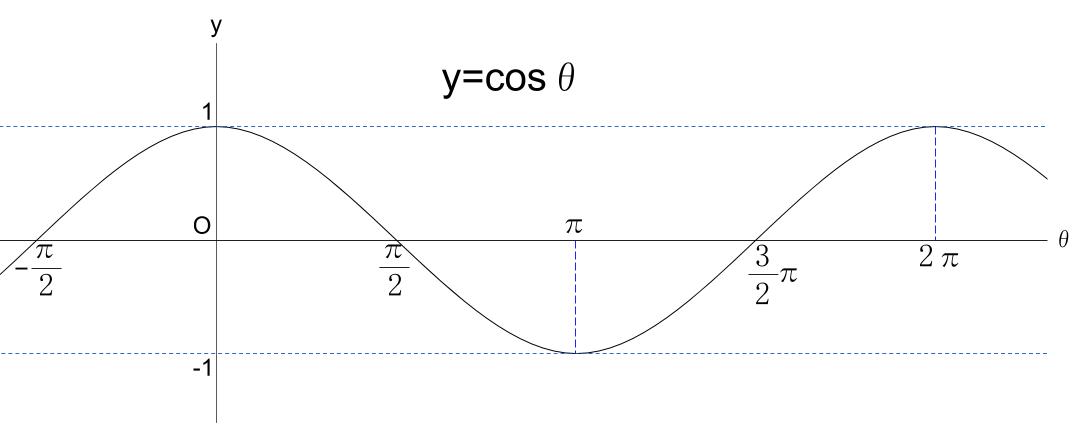
\(y=\sin \theta\) とまったく同じ曲線になります。

\(\theta\) 軸方向に\(-\displaystyle \frac{\pi}{2}\) 平行移動したグラフです。

つまり、
\(\sin (\theta+\displaystyle \frac{\pi}{2})=\cos \theta\) ということです。
もちろん
\(\cos (\theta-\displaystyle \frac{\pi}{2})=\sin \theta\) ということです。

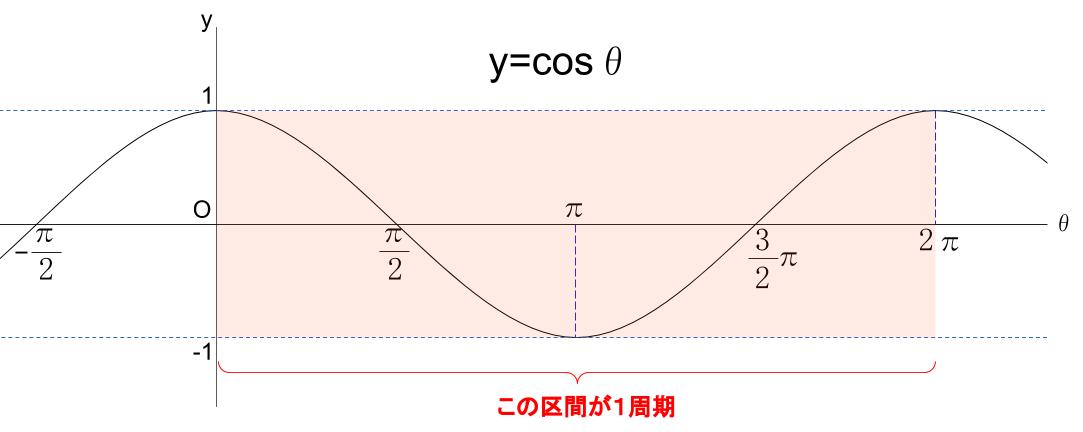
周期が \(2\pi\)
関数の値域は \(-1 \leqq y \leqq 1\)

\(y= \tan \theta\) のグラフ

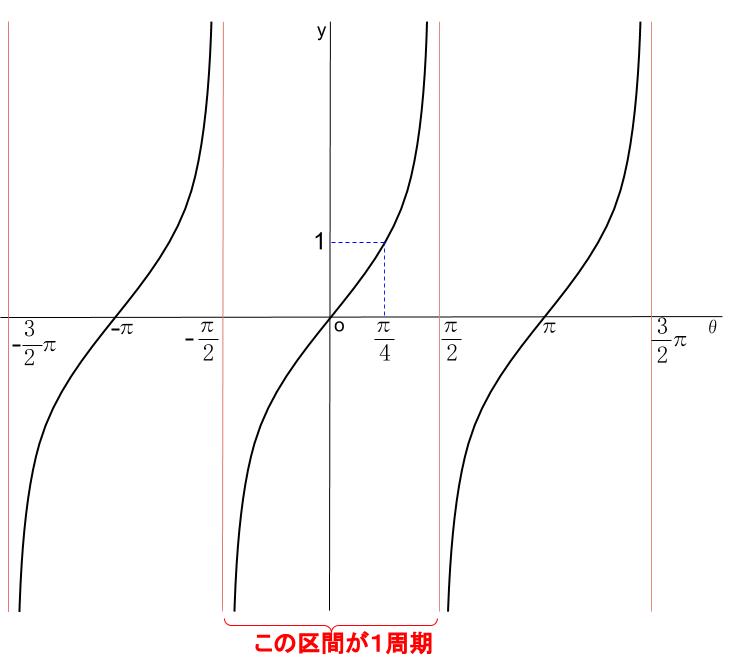
原点について対称です。
周期は \(\pi\)
値域は実数全体となります。

直線 \(\theta=\displaystyle \frac{\pi}{2}\) や

直線 \(\theta=\displaystyle \frac{3}{2}\pi\)

を漸近線にもちます。
まとめてかくと、直線 \(\theta=\displaystyle \frac{1}{2}\pi+n\pi\) （\(n\) は整数）が漸近線です。