文字係数を含む2次関数の最大・最少
文字係数を含む2次関数の最大・最少
\(2\) 次関数の最大値、最小値に関わる問題は、
放物線の頂点と、定義域の位置関係を図示します。
とにかくグラフをかくことがすべてです。
例題で見ていきましょう。
例題1
\(y=x^2-2mx+3\) \((0 \leqq x \leqq 3)\) の最大値と最小値を、次の場合について求めなさい。
(1)\(m \lt 0\)
(2)\(0 \lt m \lt 1\)
解説
グラフの概形が知りたいですね。
最大値と最小値は目で見て判断したいからです。
よって、平方完成します。
\(y=x^2-2mx+3\)
\(y=(x-m)^2-m^2+3\)
よって、放物線の頂点は \((m,-m^2+3)\) です。
(1)\(m \lt 0\)
放物線の頂点は \((m,-m^2+3)\) なので、
\(m \lt 0\) のとき、
グラフの概形は下図のようになります。
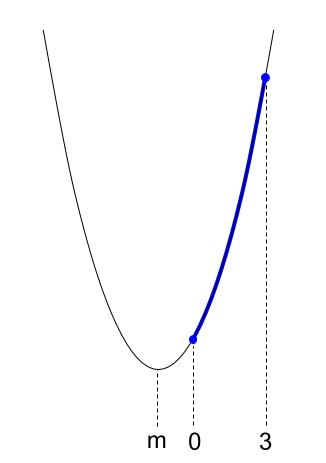
グラフが \(x\) 軸と交わるのか、交わらないのか、不確定なこともありますが、
\(0 \leqq x \leqq 3\) の最大値と最小値ならわかります。
\(x=0\) のときに最小値です。
\(y=x^2-2mx+3\) に \(x=0\) を代入して \(y=3\)
\(x=3\) のときに最大値です。
\(y=x^2-2mx+3\) に \(x=3\) を代入して \(y=-6m+12\)
つまり、
\(x=0\) のときに最小値 \(3\)
\(x=3\) のときに最大値 \(-6m+12\)
(2) \(0 \lt m \lt 1\)
放物線の頂点は \((m,-m^2+3)\) なので、
\(0 \lt m \lt 1\) のとき、
グラフの概形は下図のようになります。
定義域は \(0 \leqq x \leqq 3\) です。
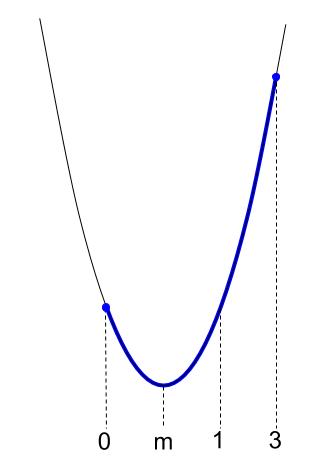
上の図では \(m\) が \(0\) と \(1\) のほぼ中間で描かれていますが、
それは不確定なことであり、 \(m\) は \(0 \lt m \lt 1\) ならば
どこにあってもかまいません。
\(2\) 次関数のグラフは左右対称なので、
軸から最も離れたところで最大値をとります。
グラフが \(x\) 軸と交わるのか、交わらないのか、
\(m\) の正確な位置など、不確定なこともありますが、
\(0 \leqq x \leqq 3\) の最大値と最小値はわかります。
グラフより、
\(x=m\) のときに最小値です。
\(y=x^2-2mx+3\) に \(x=m\) を代入して \(y=-m^2+3\)
\(x=3\) のときに最大値です。
\(y=x^2-2mx+3\) に \(x=3\) を代入して \(y=-6m+12\)
つまり、
\(x=m\) のときに最小値 \(-m^2+3\)
\(x=3\) のときに最大値 \(y=-6m+12\)
まとめ
必ず図示をして解きます。
図示をすれば、おのずと正解がでます。
これが究極のポイントですが、
放物線の頂点と、定義域の位置関係をまとめておくと
以下の \(3\) パターンあります。
以下はすべて下に凸な放物線での説明です。
上に凸も論理は同じですから省略します。
1.頂点が定義域の中央
「\(2\) 次関数のグラフは左右対称である」という重要な事実を
おさえておきましょう。
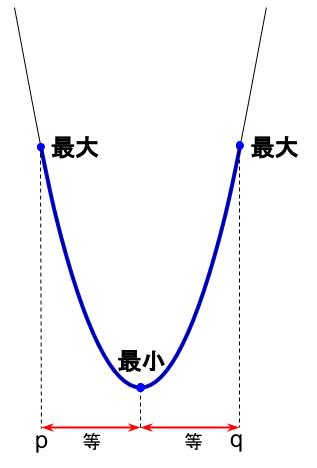
定義域は \(p \leqq x \leqq q\)
頂点が定義域の中央ならば、頂点で最小値。
最大値をとるのは、定義域の左端と右端の \(2\) つです。
2.頂点が定義域の中で中央からずれている
「\(2\) 次関数のグラフは左右対称である」なので、
頂点からより遠くはなれた定義域の端で、最大値となります。
頂点で最小値ですね。
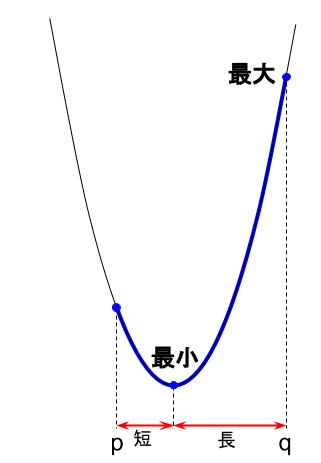
定義域は \(p \leqq x \leqq q\)
3.頂点が定義域の端か外
頂点とは無関係になります。
定義域の左右の端で、それぞれ、最大値、最小値をとります。

定義域は \(p \leqq x \leqq q\)
どれになるのか、グラフの概形をかくことで確かめましょう!