２次関数の最大・最小

関数の最大値、最小値を求める問題を学習します。
中学生のときに学習した「値域・変域」と同じものと思って
もらってＯＫです。

中学生のときも、「値域」はグラフをかいて考えましたね？
高校数学でも同様です。
数学では、「目で見ることでスッキリと解ける問題」は多く出題されます。
図示をしながら解くことが大事です。
関数の最大値、最小値は、グラフをかいて解きます！

図をかかないで、自分でもよくわからない式処理・計算をして、
結局、何が求まったのかもわからない・・・
こんな迷子になるような学習はやめましょう。
※視覚的に処理できないような概念がでてきたら、式処理で解決するのですが。

$y=x^2+4x+5$ の最小値と最大値を求めなさい。

$x$ にさまざまな値を代入したときに、さまざまな $y$ の値が得られますが、
$y$ の値の最小値と最大値はいくつになりますか？
という意味の問題です。

平方完成して、グラフの概形を知りましょう。

$y=(x+2)^2-4+5$
$y=(x+2)^2+1$

より、下図です。

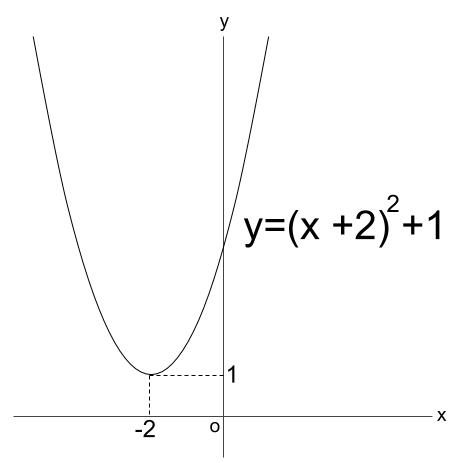
$高校数学無料学習サイトko-su- 2次関数　最大・最小1-1$

最小値は、頂点でとりますね、$1$ です。
最大値は、ありません。

こういう場合、最大値「なし」なんです。
どこまでもどこまでも大きい値をとるので、
「ここが最大です」という一点を決められないんです。
ちょっと変な感じがするかもしれませんが、最大値なしです。
覚えておきましょう。

次の関数の最小値と最大値を求めなさい。
$y=-2x^2+4x+5$　　$(2 \leqq x \leqq 4)$

平方完成して、グラフの概形を知りましょう。

$y=-2(x^2-2x)+5$
$y=-2\{(x-1)^2-1\}+5$
$y=-2(x-1)^2+2+5$
$y=-2(x-1)^2+7$

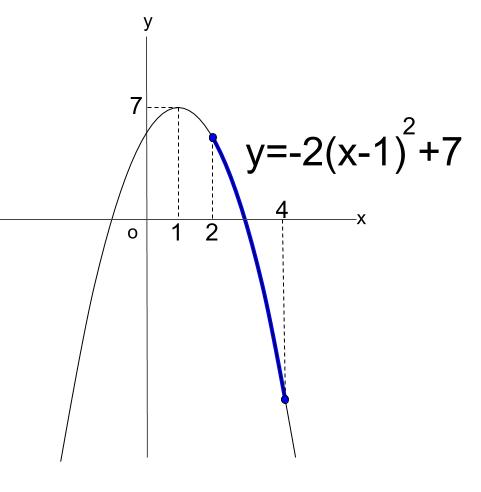
$高校数学無料学習サイトko-su- 2次関数　最大・最小1-2$

グラフは概形がわかればＯＫで、正確にかく必要はありません。

そして、定義域がどこなのかに注目します。
上図の青い太線部分です。

最小値は、$x=4$ でとり、
最大値は、$x=2$ でとることが見て取れますね。

では最小値を求めましょう。
もちろん、$y=-2x^2+4x+5$ に $x=4$ を代入して、$y$ の値を求めます。
$y=-11$ です。
最大値は、$y=-2x^2+4x+5$ に $x=2$ を代入して、$y$ の値を求めます。
$y=5$ です。