三角不等式

三角関数を含む不等式を、三角不等式といいます。
まず、不等号を\(=\) （イコール）とおいた三角方程式を解きます。
次に単位円を見て、不等式を満たす \(\theta\) の値の範囲を求めましょう。

例題１

\(0 \leqq \theta \lt 2\pi\) のとき、次の不等式を解きなさい。
\(2\sin \theta+\sqrt{3} \leqq 0\)

解説

等式を満たす \(\theta\) の値の範囲を求めることが目標です。

\(2\sin \theta+\sqrt{3} \leqq 0\) を変形して

\(\sin \theta \leqq -\displaystyle \frac{\sqrt{3}}{2}\)

単位円で図示します。
\(\sin \theta\) は単位円周上の \(y\) 座標です。

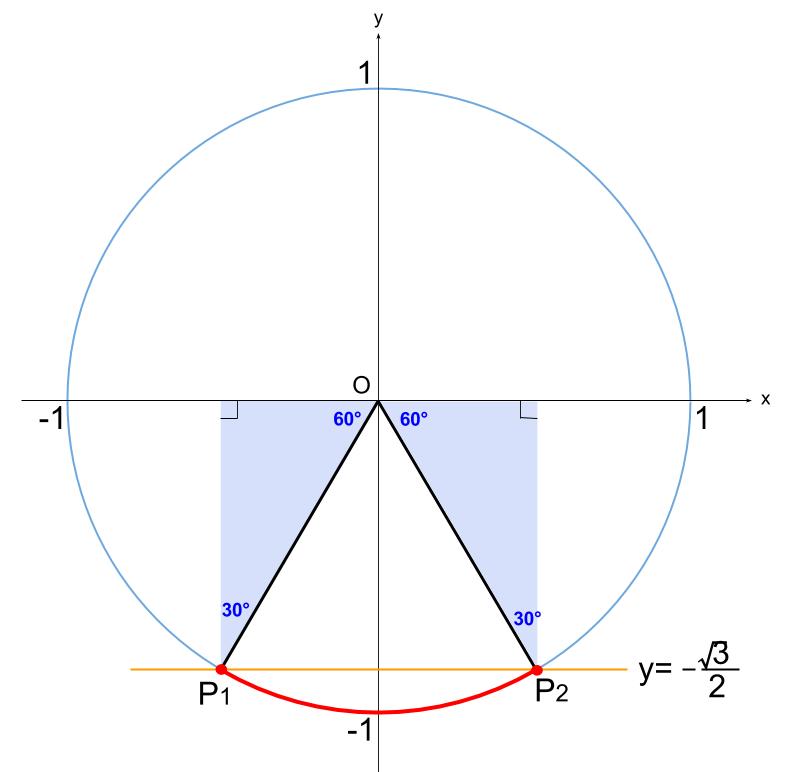
図の赤い太線部分が、不等式を満たす範囲なので、
\(0 \leqq \theta \lt 2\pi\) より、

\(\displaystyle \frac{4}{3}\pi \leqq \theta \leqq \displaystyle \frac{5}{3}\pi\)

例題２

\(0 \leqq \theta \lt 2\pi\) のとき、次の不等式を解きなさい。
\(2\cos \theta \gt -\sqrt{2}\)

解説

等式を満たす \(\theta\) の値の範囲を求めることが目標です。

\(2\cos \theta \gt -\sqrt{2}\) を変形して

\(\cos \theta \gt -\displaystyle \frac{\sqrt{2}}{2}\)

単位円で図示します。
\(\cos \theta\) は単位円周上の \(x\) 座標です。

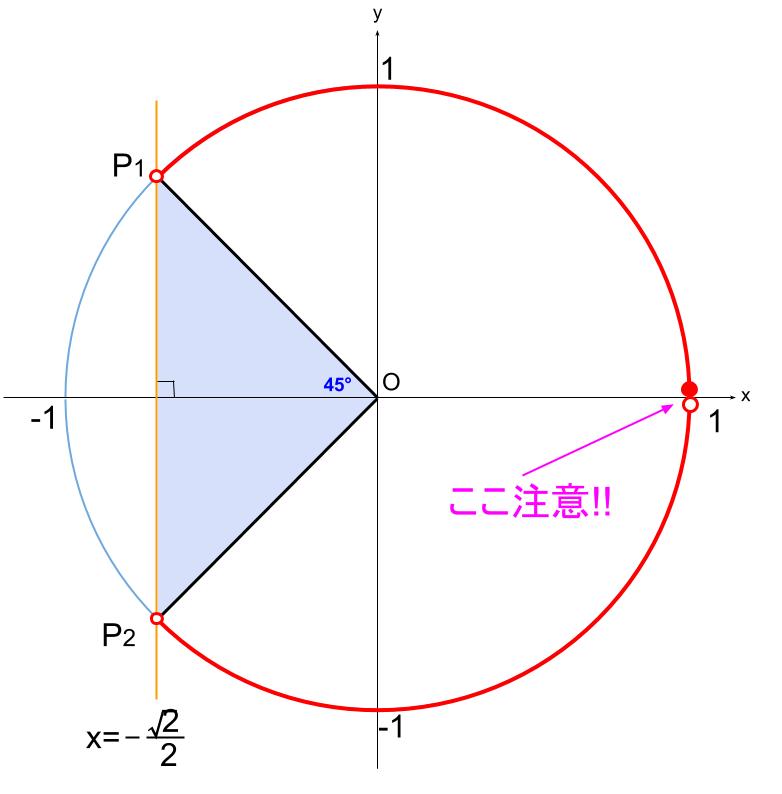
図の赤い太線部分が、不等式を満たす範囲なので、
\(0 \leqq \theta \lt 2\pi\) より、

\(0 \leqq \theta \lt \displaystyle \frac{3}{4}\pi\) 、\(\displaystyle \frac{5}{4}\pi \lt \theta \lt 2\pi\)
※ \(2\pi\) を含まない範囲です。等号なのか不等号なのか注意しましょう。

例題３

\(0 \leqq \theta \lt 2\pi\) のとき、次の不等式を解きなさい。
\(\tan \theta \geqq -1\)

解説

等式を満たす \(\theta\) の値の範囲を求めることが目標です。

単位円で図示します。
\(\tan \theta\) は直線の傾きです。
直線の傾きが \(-1\) より大きくなる範囲を考えます。

「傾きが大きい」という言葉につられると、傾斜を急にしたくなりますが、
要注意です。
直線の傾きが \(-1\) より大きいとは、

例えば、直線の傾きが \(-\displaystyle \frac{1}{2}\) です。

これは傾斜が緩やかになります。
傾きが負の範囲は慎重に進めていきましょう。

そしてもちろん直線の傾きが正の範囲も直線の傾きが \(-1\) より大きいです。

よって、下図のようになります。

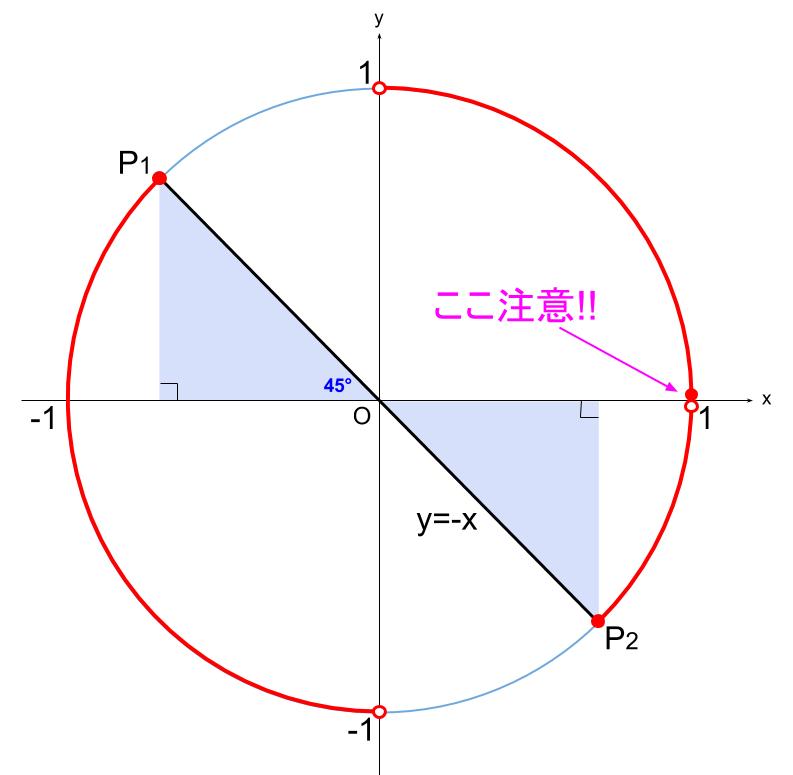
図の赤い太線部分が、不等式を満たす範囲なので、
\(0 \leqq \theta \lt 2\pi\) より、
\(0 \leqq \theta \lt \displaystyle \frac{\pi}{2}\) 、\(\displaystyle \frac{3}{4}\pi \leqq \theta \lt \displaystyle \frac{3}{2}\pi\)、 \(\displaystyle \frac{7}{4}\pi\ \leqq \theta \lt 2\pi\)
※ \(2\pi\) を含まない範囲です。等号なのか不等号なのか注意しましょう。
※\(\tan \theta\) は、\(\theta=\displaystyle \frac{\pi}{2}、\displaystyle \frac{3}{2}\pi\) で定義されません。

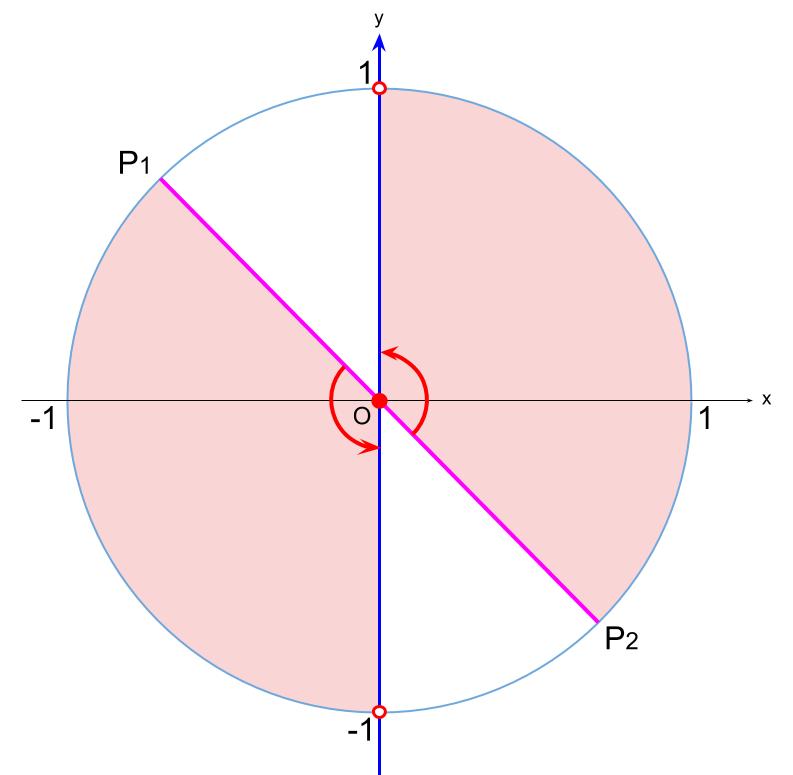
別解・\(\tan\) の傾きの範囲

\(\tan \theta\) が小さい範囲は時計まわりの範囲、
\(\tan \theta\) が大きい範囲は反時計まわりの範囲、
と覚えましょう。
不等号を等号にしたときの直線を、原点 \(O\) を中心に回転させます。
\(y\) 軸にぶつかるまで回しましょう。

例 ：\(\tan \theta \gt -1\) の範囲
より大きい範囲は「反時計まわり」です。