三角方程式・不等式(2次式)
ポイント
\(\sin^2 \theta +\cos^2 \theta =1\)
を用いて、\(\sin \theta\) あるいは \(\cos \theta\) だけの \(2\) 次式にします。
その後は \(\sin \theta=t\) あるいは \(\cos \theta=t\) などと置き換えて、
\(t\) の \(2\) 次方程式(不等式)の処理です。
ただし、\(t\) の取り得る値の範囲に注意しましょう。
例題1
\(0 \leqq \theta \lt 2\pi\) のとき、次の方程式 を解きなさい。
\(2\cos^2 \theta-5\sin \theta+1=0\)
解説
\(2 \cos^2 \theta-5\sin \theta+1=0\) を
\(\sin^2 \theta +\cos^2 \theta =1\)を用いて \(\sin \theta\) だけの式にします。
※ \(\cos^2 \theta\) は変形できますが、\(5\sin \theta\) は変形できません。
\(\sin \theta\) だけの式にするのが良いですね。
与式は
\(2(1-\sin^2 \theta)-5\sin \theta+1=0\)
\(-2\sin^2\theta-5\sin \theta+3=0\)
両辺に \(-1\) をかけて、
\(2\sin^2\theta+5\sin \theta-3=0\)・・・①
ここで、\(\sin \theta=t\) とおくと、\(-1 \leqq t \leqq 1\) ・・・②
①は、
\(2t^2+5t-3=0\)
この \(2\) 次方程式を解きます。
因数分解して、
\((2t-1)(t+3)=0\)
より、\(t=\displaystyle \frac{1}{2},-3\)
\(t=-3\) は②の \(-1 \leqq t \leqq 1\) を満たさないため不適。
よって、\(0 \leqq \theta \lt 2\pi\) で \(t=\displaystyle \frac{1}{2}\)
つまり、\(\sin \theta=\displaystyle \frac{1}{2}\) を解きます。
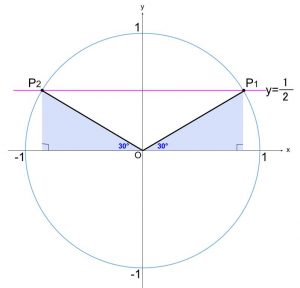
よって、\(\theta =\displaystyle \frac{\pi}{6},\displaystyle \frac{5}{6}\pi\)
これで解決です!
例題2
\(0 \leqq \theta \lt 2\pi\) のとき、次の方程式 を解きなさい。
\(2\sin^2 \theta-\cos \theta-1=0\)
解説
\(2\sin^2 \theta-\cos \theta-1=0\) を
\(\sin^2 \theta +\cos^2 \theta =1\)を用いて \(\cos \theta\) だけの式にします。
※ \(\sin^2 \theta\) は変形できますが、\(\cos \theta\) は変形できません。
\(\cos \theta\) だけの式にするのが良いですね。
与式は
\(2(1-\cos^2 \theta)-\cos \theta-1=0\)
\(-2\cos^2\theta-\cos \theta+1=0\)
両辺に \(-1\) をかけて、
\(2\cos^2\theta+\cos \theta-1=0\)・・・①
ここで、\(\cos \theta=t\) とおくと、\(-1 \leqq t \leqq 1\) ・・・②
①は、
\(2t^2+t-1=0\)
この \(2\) 次方程式を解きます。
因数分解して、
\((t+1)(2t-1)=0\)
より、\(t=-1,\displaystyle \frac{1}{2}\)
これは、いずれも②の \(-1 \leqq t \leqq 1\) を満たします。
よって、\(0 \leqq \theta \lt 2\pi\) で
\(t=-1\) と \(t=\displaystyle \frac{1}{2}\) を解きます。
つまり、
\(\cos \theta=-1\) を解いて、\(\theta =\pi\)
\(\cos \theta=\displaystyle \frac{1}{2}\) を解いて、\(\theta =\displaystyle \frac{\pi}{3},\displaystyle \frac{5}{3}\pi\)
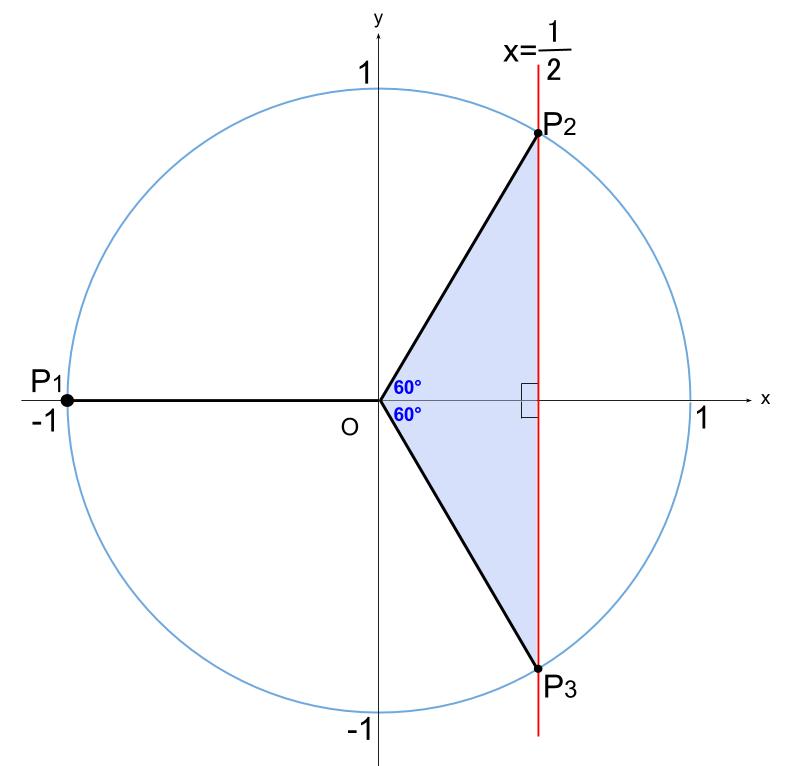
よって、\(\theta =\displaystyle \frac{\pi}{3},\pi,\displaystyle \frac{5}{3}\pi\)
例題3
\(0 \leqq \theta \lt 2\pi\) のとき、次の不等式 を解きなさい。
\(2\cos^2 \theta \geqq 3\sin \theta\)
解説
\(2\cos^2 \theta \geqq 3\sin \theta\) を
\(\sin^2 \theta +\cos^2 \theta =1\)を用いて \(\sin \theta\) だけの式にします。
\(2(1-\sin^2 \theta)-3\sin \theta \geqq 0\)
\(-2\sin^2\theta-3\sin \theta+2 \geqq 0\)
両辺に \(-1\) をかけて、
\(2\sin^2\theta+3\sin \theta-2 \leqq 0\)・・・①
※不等号の向きが変わります。注意!
ここで、\(\sin \theta=t\) とおくと、\(-1 \leqq t \leqq 1\) ・・・②
①は、
\(2t^2+3t-2 \leqq 0\)
この \(2\) 次不等式を解きます。
因数分解して、
\((2t-1)(t+2) \leqq 0\)
より、\(-2 \leqq t \leqq \displaystyle \frac{1}{2}\) ・・・③
②、③より、 \(-1 \leqq t \leqq \displaystyle \frac{1}{2}\)
よって、\(0 \leqq \theta \lt 2\pi\) で
\(-1 \leqq \sin \theta \leqq \displaystyle \frac{1}{2}\) を解きます。
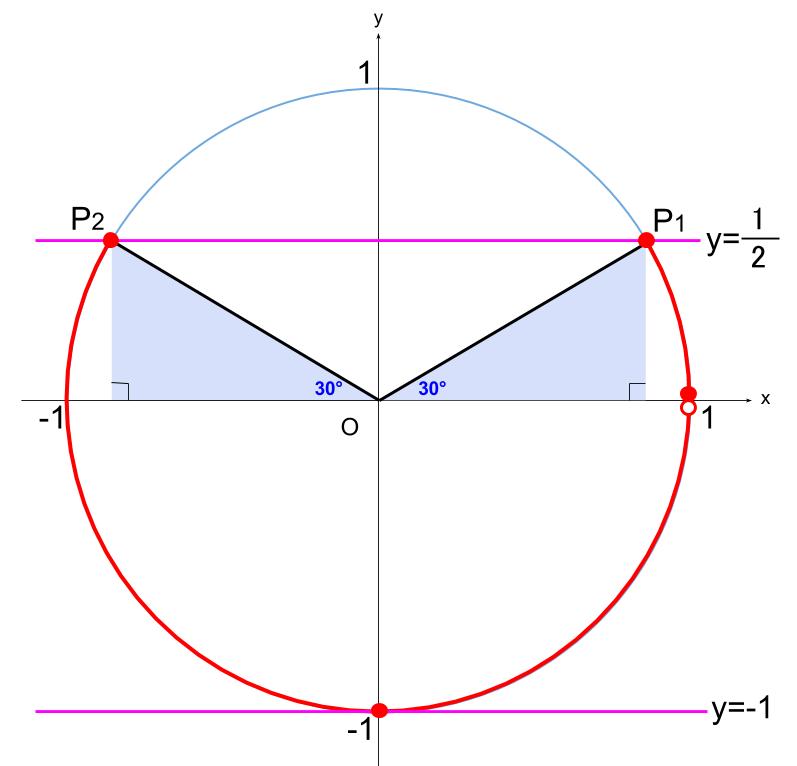
図より、
\(0 \leqq \theta \leqq \displaystyle \frac{\pi}{6},\displaystyle \frac{5}{6}\pi \leqq \theta \lt 2\pi\)