絶対値

数直線上で、実数 \(a\) に対応する点と原点との距離を絶対値といい、\(|a|\) で表します。

\(|4|=4\)
\(|-4|=4\)

つまり、

例題１

次の式の値を求めなさい。

（１）\(|1-\displaystyle \frac{5}{3}|\)

（２）\(|1-\pi|\)

解説

\(|1-\displaystyle \frac{5}{3}|\)

\(|1-\displaystyle \frac{5}{3}|=|-\displaystyle \frac{2}{3}|=\displaystyle \frac{2}{3}\)

（２）\(|1-\pi|\)

\(\pi \fallingdotseq 3.14\) なので、
※およそ等しい、という記号です。
\(1-\pi\) は負の値です。

\( a \lt 0 \) のとき、 \(| a | = -a \) なので、
\(|1-\pi|=-(1-\pi)=\pi-1\)

例題２

\(a=3\) のとき、\(| a-1 | +| a-5 | \) の値を求めなさい。

解説

\(a=3\) を代入するだけです。

\(| 3-1 | +| 3-5 |=| 2 | +| -2 |=2+2=4 \)

平方根と絶対値

\(2\) 乗すると、符号が必ず正になります。
絶対値は必ず正の値なので、以下のように関連づけられます。

\(\sqrt{(3)^2}=\sqrt{9}=3\)
\(\sqrt{(-3)^2}=\sqrt{9}=3\)

つまり、\(\sqrt{(a)^2}\) は、 \(a\) の符号を正にする計算操作であり、

\(\sqrt{(a)^2}=|a|\)
といえます。

例題１

次の式を簡単にしなさい。

\(\sqrt{(a+1)^2}+\sqrt{(a-3)^2}\)
ただし、\(-1 \lt a \lt 3\)

解説

\(\sqrt{(a)^2}=|a|\) を使います。解法暗記としか言いようがありません。

\(\sqrt{(a+1)^2}+\sqrt{(a-3)^2}=|a+1|+|a-3|\)・・・①
\(-1 \lt a \lt 3\) のとき、
\(a+1 \gt 0\)
\(a-3 \lt 0\)
より、\( |a+1|=a+1\)
\(|a-3|=-(a-3)=-a+3\)

よって①より、
（与式）\(=a+1+(-a+3)=4\)

例題２

次の式を簡単にしなさい。

\(\sqrt{(a+2)^2}+\sqrt{(a-1)^2}\)　　

解説

もちろん、\(\sqrt{(a)^2}=|a|\) を使います。

\(\sqrt{(a+2)^2}+\sqrt{(a-1)^2}=|a+2|+|a-1|\)

ここで \(a\) の値によって場合分けが必要になります。

\(\begin{eqnarray}| a+2 | = \begin{cases} a+2 & ( a \geqq -2 ) \\ -(a+2) & ( a \lt -2 ) \end{cases}\end{eqnarray}\)

\(\begin{eqnarray}| a-1 | = \begin{cases} a-1 & ( a \geqq 1 ) \\ -(a-1) & ( a \lt 1 ) \end{cases}\end{eqnarray}\)

なので、
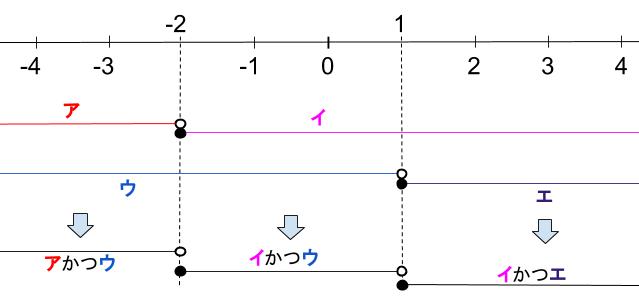
\(a \lt -2\)
\(-2 \leqq a \lt 1\)
\(1 \leqq a\)
の \(3\) つの範囲に分ける必要があります。

\(a \lt -2\)

\(a \lt -2\) のとき
\(|a+2|+|a-1|=-(a+2)+\{-(a-1)\}\)
\(=-a-2-a+1\)
\(=-2a-1\)

\(-2 \leqq a \lt 1\)

\(-2 \leqq a \lt 1\) のとき
\(|a+2|+|a-1|=a+2+\{-(a-1)\}\)
\(=a+2-a+1\)
\(=3\)

\(1 \leqq a\)

\(1 \leqq a\) のとき
\(|a+2|+|a-1|=a+2+(a-1)\)
\(=a+2+a-1\)
\(=2a+1\)