約数の個数

素数が \(2,3\) 種類で分解されたときが上です。
もっと多くても構いません。とにかく具体例を見ましょう。

\(200\) の約数の個数は、
\(200=2^3×5^2\) なので、
\((3+1)(2+1)=12\) 個

\(600\) の約数の個数は、
\(600=2^3×3×5^2\) なので、
\((3+1)(1+1)(2+1)=24\) 個

\(2100\) の約数の個数は、
\(2100=2^2×3×5^2×7\) なので、
\((2+1)(1+1)(2+1)(1+1)=36\) 個

なぜ？約数の個数の公式

\(18\) の約数がいくつあるのか。これで公式の意味を理解しましょう。

\(18\) の約数をかき出すと、\(1,2,3,6,9,18\) の \(6\) 個あります。

この \(6\) 個が、素因数分解から導かれる理由は以下のようになります。

\(18=2×3^2\) ですが、\(18\) の約数 \(A\) は \(A=2^p ×3^q\) とかけます。
そして、\(p=0,1\) であり、\(q=0,1,2\) です。

つまり、\(p\) が\(2\) 通り、\(q\) が \(3\) 通りなので、

\(2×3=6\) 個の約数があります。

\(1=2^0 ×3^0\)
\(3=2^0 ×3^1\)
\(9=2^0 ×3^2\)
\(2=2^1 ×3^0\)
\(6=2^1 ×3^1\)
\(18=2^1 ×3^2\)

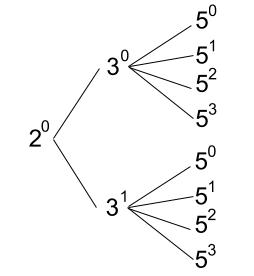
これは樹形図にするのがわかりやすいでしょう。

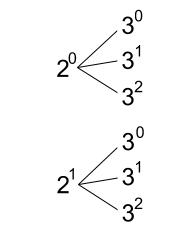
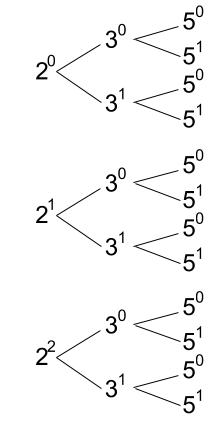
素因数の数が増えても同様です。
例えば、\(60\) の約数は、
\(1,2,3,4,5,6,10,12,15,20,30,60\) の \(12\) 個です。

\(60=2^2×3×5\) ですが、\(60\) の約数 \(B\) は \(B=2^p ×3^q×5^r\) とかけます。
そして、\(p=0,1,2\) であり、\(q=0,1\) であり、\(r=0,1\) です。

つまり、\(p\) が\(3\) 通り、\(q\) が \(2\) 通り、\(r\) が \(2\) 通りなので、

\(3×2×2=12\) 個の約数があります。

例題１

\(1500\) の約数の個数は全部で何個ですか。またその中で、奇数であるのは何個ですか。

解説

\(1500=2^2×3×5^3\)

より、\((2+1)(1+1)(3+1)=24\) 個

次に奇数の約数の個数です。
\(1500\) の約数は \(2^p×3^q×5^r\) とかけますが、奇数になるのは、\(p=0\)、つまり \(2\) が \(1\) つも使われないときです。

よって、\(q,r\) の要素だけ考えて、
\((1+1)(3+1)=8\) 個