底の変換公式

\(0 \lt a,0 \lt b,0 \lt c\) で、\(a \neq\ 1, c \neq 1\) のとき、
※つまり、底は１でなく０より大、真数は０より大のとき

\(\log_{ a } b=\displaystyle \frac{\log_{ c } b}{\log_{ c } a}\)

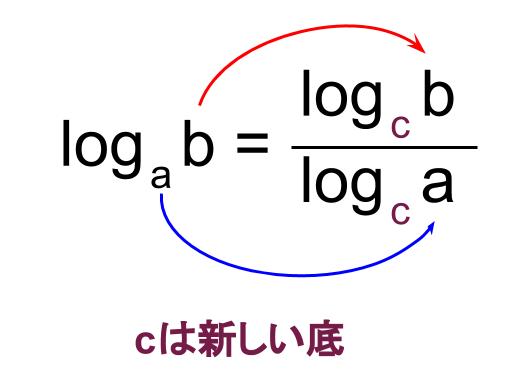
これを底の変換公式といいます。
不思議な公式ですね。

\(0 \lt c\) ならばどんな値でもＯＫです。
与えられた対数を、好きな底 \(c\) で表し直すことができます。

これも証明はひとまず保留します。
最重要事項は、この公式が体にしみこみ、
考えることなく使いこなせるようになることだからです。

例

次の値を求めなさい。
\(\log_{ 8 } 256\)

解説

\(8\) も \(256\) も \(2^n\) の形に簡単に変形できます。
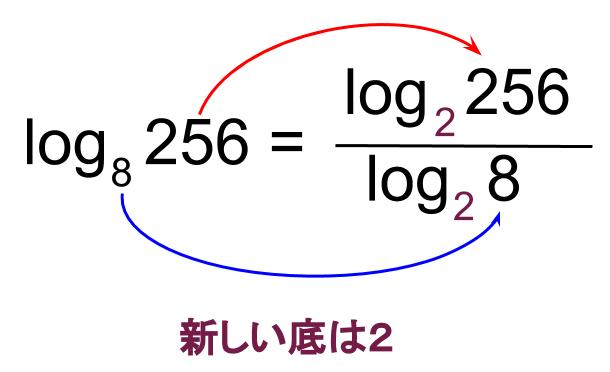
新しい底は、\(2\) にしたら良さそうです。

\(\log_{ 8 } 256=\displaystyle \frac{\log_{ 2 } 256}{\log_{ 2 } 8}\)

\(=\displaystyle \frac{\log_{ 2 } 2^8}{\log_{ 2 } 2^3}\)

\(=\displaystyle \frac{8}{3}\)

別解１

実は・・・新しい底はいくつであっても解けます。
例えば、\(5\) を新しい底として計算してみると・・・

\(\log_{ 8 } 256=\displaystyle \frac{\log_{ 5 } 256}{\log_{ 5 } 8}\)

\(=\displaystyle \frac{\log_{ 5 } 2^8}{\log_{ 5 } 2^3}\)

\(=\displaystyle \frac{8\log_{ 5 } 2}{3\log_{ 5 } 2}\)

\(=\displaystyle \frac{8}{3}\)

結局は真数を \(2^a\) に変形するということが本質だったわけです。
新しい底がいくつであっても、いずれも同じ解き方です。

別解２

ところでこれって指数法則でも解けますよね。

\(\log_{ 8 } 256=x\) とおくと、

\(8^x=256\)
\((2^3)^x=2^8\)
\(2^{3x}=2^8\)
よって、
\(3x=8\)

\(x=\displaystyle \frac{8}{3}\)

例題２

次の値を求めなさい。
\(\log_{ 8 } 25 \cdot \log_{ 5 } 2\)

解説

何をしたらいいのか、ゴールまでの道は見えなくとも、

底をそろえたら計算が進みそうだな、という感覚があればＯＫです。

それを、実際にやってみるのです。

「高校数学」の基本姿勢の \(1\) つと言えます。

\(25\) と \(5\) があるので、
底を \(5\) にそろえて見ましょう。

\(\displaystyle \frac{\log_{ 5 } 25}{\log_{ 5 } 8 } \cdot \log_{ 5 } 2\)

\(=\displaystyle \frac{\log_{ 5 } 5^2}{\log_{ 5 } 2^3 } \cdot \log_{ 5 } 2\)

\(=\displaystyle \frac{2}{3\log_{ 5 } 2 } \cdot \log_{ 5 } 2\)

\(=\displaystyle \frac{2}{3}\)

※実は本問も、底をいくつにそろえても計算可能です。
底を \(a\) に変換して解いてみましょう。

\(\log_{ 8 } 25 \cdot \log_{ 5 } 2\)

\(=\displaystyle \frac{\log_{ a } 5^2}{\log_{ a } 2^3 }×\displaystyle \frac{\log_{ a } 2}{\log_{ a } 5 }\)

\(=\displaystyle \frac{2\log_{ a } 5}{3\log_{ a } 2 }×\displaystyle \frac{\log_{ a } 2}{\log_{ a } 5 }\)

\(=\displaystyle \frac{2}{3}\)

底の変換公式の証明

とても不思議な底の変換公式の証明を見ておきましょう。
証明は自力でできた方がいいですが、あまりこだわる必要はありません。

とても便利な計算公式！と割り切って、計算上手になることの方が学習の
優先度は高いです。

ちなみに
\(5=2^x\) のとき
\(x=\log_{ 2 } 5\) なので、
\(2^{\log_{ 2 } 5} =5\)
です。

つまり
\(a^{\log_{ a } M} =M\)ですね。
これを利用します。

では \(\log_{ a } M\) の底を \(c\) に変換してみましょう。

\(\log_{ a } M=\displaystyle \frac{\log_{ c } M}{\log_{ c } a}\)

を示すのが最終目標です。

底の変換公式の導出！

\(a^{\log_{ a } M}=M\)
の対数を、底を \(c\) でとると

\(\log_{ c } a^{\log_{ a } M}=\log_{ c } M\)

\(\log_{ a } M \cdot \log_{ c } a= \log_{ c } M\)

\(\log_{ a } M=\displaystyle \frac{\log_{ c } M}{\log_{ c } a}\)

これで示せました。