対称式・交代式の因数分解

対称式

\(a,b,c\) の多項式で、\(a,b,c\) のどの \(2\) つの文字を入れかえても、もとの式と同じ式になるものを対称式といいます。

対称式の例
\(a+b+c\)
\(ab+bc+ca\)
\(ca\) という項は、アルファベット順の \(ac\) になっていません。
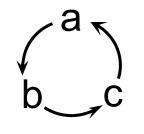
これは、下図のように、\(a,b,c\) が輪の形に循環するような順序で整理しているからです。
これを、輪環の順に整理するといいます。

交代式

\(a,b,c\) の多項式で、\(a,b,c\) のどの \(2\) つの文字を入れかえても、もとの式と符号だけが異なる式になるものを交代式といいます。

交代式の例
\((a-b)(b-c)(c-a)\)

対称式・交代式の因数分解

対称式、交代式とは何かについて、説明をしてきましたが、
対称式、交代式を因数分解するときに、特有のコツやテクニックがあるわけではありません。

対称式・交代式は、各文字の次数が等しいので、因数分解するときは、どれでもいいので、\(1\) つの文字について整理します。

例題１

\(ab(a+b)+bc(b+c)+ca(c+a)+2abc\) を因数分解しなさい。

解説

一見して、\(a,b,c\) について、きれいな対称的な式ですね。きっと対称式か交代式なのでしょう。

どちらであるか（あるいはどちらでもないか）を判別する必要などありません。

因数分解するのですから、文字の次数がどうなっているかを確認します。

すべての文字について同じ次数なので、どれでもいいので、\(1\) つの文字について整理します。

では、 \(a\) について整理しましょう。

\(ab(a+b)+bc(b+c)+ca(c+a)+2abc\)

\(=a^2b+ab^2+bc(b+c)+c^2a+ca^2+2abc\)

\(=(b+c)a^2+(b^2+2bc+c^2)a+bc(b+c)\)

\(=(b+c)a^2+(b+c)^2a+bc(b+c)\)

\(=(b+c)\{a^2+(b+c)a+bc\}\)

\(=(b+c)(a+b)(a+c)\)

\(=(a+b)(b+c)(c+a)\)

輪環の順です。

例題２

\(a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)\) を因数分解しなさい。

解説

すべての文字について同じ次数なので、どれでもいいので、\(1\) つの文字について整理します。

では、 \(a\) について整理しましょう。

\(a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)\)
\(=a(b^2-c^2)+bc^2-a^2b+ca^2-b^2c\)
\(=(c-b)a^2+(b^2-c^2)a+bc^2-b^2c\)
\(=(c-b)a^2+(b+c)(b-c)a+bc(c-b)\)
\(=(c-b)a^2-(b+c)(c-b)a+bc(c-b)\)
\(=(c-b)\{a^2-(b+c)a+bc\}\)
\(=(c-b)(a-b)(a-c)\)
\(=(a-b)(b-c)(c-a)\)

参考

対称式は因数分解しても対称式であり、
交代式は因数分解しても交代式のままです。

また、
対称式は \((a+b)\) を因数として持つならば、\((b+c)(c+a)\) を因数としてもちます。
交代式は \((a-b)(b-c)(c-a)\) を因数にもちます。