文字係数のたすきがけ因数分解

前ページで \(x\) の \(2\) 次式において、定数項が \(y\) の \(2\) 次式というものを扱いました。

さらに発展させれば、それの「たすき掛け因数分解」となります。

例えば、
\((2x+2y+1)(x+y-3)\)
を展開すると
\((2x+2y+1)(x+y-3)\)
\(=\{2x+(2y+1)\}\{x+(y-3)\}\)
\(=2x^2+\{(2y+1)+2(y-3)\}x+(2y+1)(y-3)\)
\(=2x^2+(4y-5)x+(2y+1)(y-3)\)
です。

この計算の逆を行うのです。
\(2x^2+(4y-5)x+(2y+1)(y-3)\) を因数分解しなさい。

やり方は、今までのたすき掛け因数分解のやり方をそのままやるだけです。

具体例を見ていきましょう。

例題１

次の式を因数分解しなさい。
\(ax^2-(a^2-1)x-a\)

解説

一見して方針がたたないかもしれませんが、\(x\) について降べきの順に整理されています。
公式が適用できないので、たすきがけです。

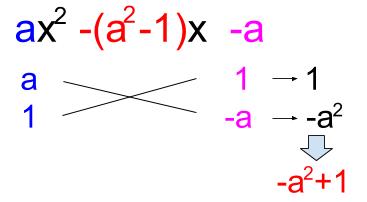
よって、\(a,1,1,-a\) の順に並べて因数分解完了です。
\(ax^2-(a^2-1)x-a=(ax+1)(1x-a)\)
\(=(ax+1)(x-a)\)

例題２

次の式を因数分解しなさい。
\(3x^2-(4a+1)x-4a^2+2a\)

解説

\(x\) について降べきの順に整理されています。
公式が適用できないので、たすきがけをしましょう。
つまり、定数項が因数分解されるはずですが・・・

\(3x^2-(4a+1)x-4a^2+2a\)
\(=3x^2-(4a+1)x-2a(2a-1)\)

案の定、定数項が因数分解されました。
よって、
\(-2a×(2a-1)\)
か
\(2a×\{-(2a-1)\}\)
のいずれかでたすき掛けが成功するに違いありません。
計算してうまくいくものを探すのみです。

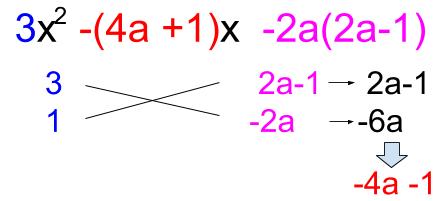
よって、\(3,2a-1,1,-2a\) の順に並べて因数分解完了です。
\(3x^2-(4a+1)x-4a^2+2a\)
\(=3x^2-(4a+1)x-2a(2a-1)\)
\(=(3x+2a-1)(1x-2a)\)
\(=(3x+2a-1)(x-2a)\)

例題３

次の式を因数分解しなさい。
\(2x^2+xy-y^2+5x-4y-3\)

解説

最も次数の低い文字について、降べきの順に整理します。
\(x,y\) どちらも同じ次数です。

\(x\) について整理

\(x\) について整理すると
\(2x^2+xy-y^2+5x-4y-3\)
\(=2x^2+(y+5)x-y^2-4y-3\)
\(=2x^2+(y+5)x-(y^2+4y+3)\)
\(=2x^2+(y+5)x-(y+1)(y+3)\)
※ここでたすき掛け因数分解です。

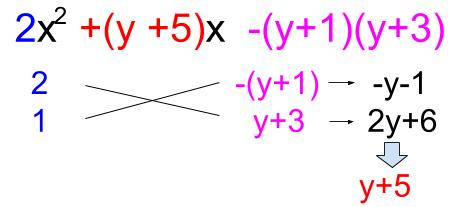
\(=\{2x-(y+1)\}\{x+(y+3)\}\)
\(=(2x-y-1)(x+y+3)\)

\(y\) について整理

\(y\) について整理すると
\(2x^2+xy-y^2+5x-4y-3\)
\(=-y^2+(x-4)y+2x^2+5x-3\)
\(=-\{y^2-(x-4)y-2x^2-5x+3\}\)
\(=-\{y^2-(x-4)y-(2x^2+5x-3)\}\)
※ここで定数項をたすき掛け因数分解です。
\(=-\{y^2-(x-4)y-(2x-1)(x+3)\}\)
\(=-(y-2x+1)(y+x+3)\)
\(x,y\) の順で並べましょう。

\(-(y-2x+1)(y+x+3)\)
\(=(2x-y-1)(x+y+3)\)

どちらの文字で整理してもたすきがけ因数分解から逃れられません。
どのタイミングでたすきがけになるかが異なります。
自分が解きやすいほうでどうぞ。
どちらで解いても楽勝！というのがベストです。

例題４

次の式を因数分解しなさい。
\(2x^2-7xy+3y^2-5x+5y+2\)

解説

\(x,y\)、まずどちらで整理しても最後にたすきがけ因数分解から逃れられません。
どちらの文字で整理してもいいのですね。

\(x\) について整理

\(x\) について整理すると
\(2x^2-7xy+3y^2-5x+5y+2\)
\(=2x^2-(7y+5)x+3y^2+5y+2\)

定数項を因数分解します。たすきがけですね。

\(2x^2-(7y+5)x+3y^2+5y+2\)
\(=2x^2-(7y+5)x+(3y+2)(y+1)\)

そして、もう一度たすきがけです。

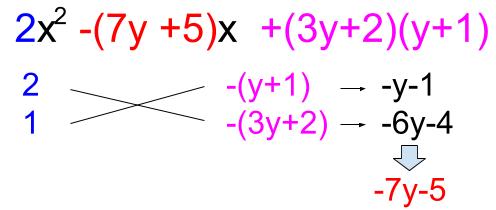
よって、
\(2x^2-(7y+5)x+(3y+2)(y+1)\)
\(=\{(2x-(y+1)\}\{(x-(3y+2)\}\)
\(=(2x-y-1)(x-3y-2)\)

\(y\) について整理

\(y\) について整理すると
\(2x^2-7xy+3y^2-5x+5y+2\)
\(=3y^2-(7x-5)y+2x^2-5x+2\)

定数項を因数分解します。たすきがけですね。

\(3y^2-(7x-5)y+2x^2-5x+2\)
\(=3y^2-(7x-5)y+(2x-1)(x-2)\)

そして、もう一度たすきがけです。

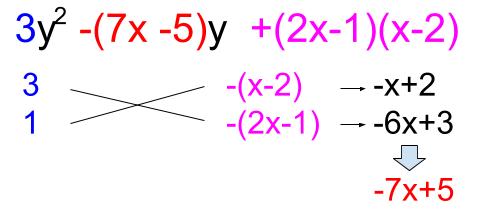
よって
\(=3y^2-(7x-5)y+(2x-1)(x-2)\)
\(=\{3y-(x-2)\}\{y-(2x-1)\}\)
\(=(3y-x+2)(y-2x+1)\)
\(x,y\) の順で並べると
\((3y-x+2)(y-2x+1)\)
\(=(-x+3y+2)(-2x+y+1)\)
\(=-(x-3y-2)\{-(2x-y-1)\}\)
\(=(x-3y-2)(2x-y-1)\)