接弦定理
姉妹サイト「中学数学サイトchu-su-」と同じ内容です。
接弦定理
円と接線と弦のつくる角の定理なので、接弦定理という名前がついていますが、
円と接線と、「内接三角形」のときに用いる定理と覚えるのが良いでしょう。
とにかく図で覚えます。
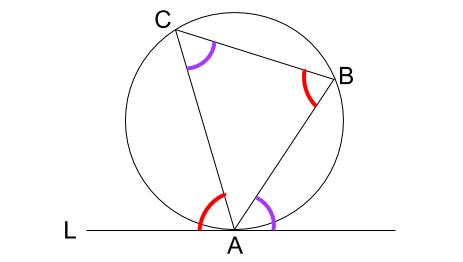
直線 \(L\) が点 \(A\) で接しているとき、下図のように角が等しくなる。
同じ色の角は等しい。
例1
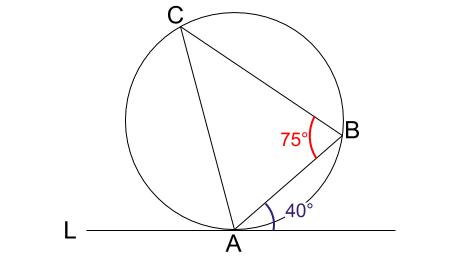
直線 \(L\) が点 \(A\) で接しているとき、角 \(\angle CAB\) を求めなさい。
解答
接弦定理より、点 \(A\) の左の角の大きさは、\(\angle B\) の大きさと等しく \(75°\)
\(\angle CAB=180-(40+75)=65°\)
接弦定理の証明
なぜ接弦定理が成り立つのか見ていきましょう。
円があれば、その中心から補助線を引きます。
そうすれば、図形的性質が明らかになります。
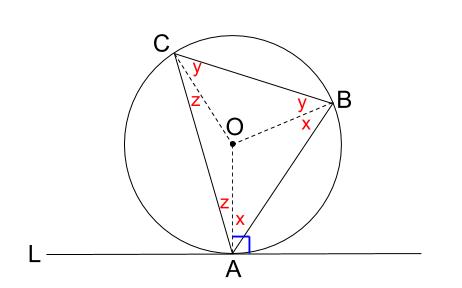
半径を辺とする二等辺三角形が \(3\) つできます。
その底角をそれぞれ \(x,y,z\) とおきました。
三角形 \(ABC\) の内角の和より、
\(2x+2y+2z=180°\)
より、
\(x+y+z=90°\)
が成り立ちます。
また、\(OA\) と \(L\) は垂直です。
よって、下図のピンク色の角の大きさは \(y+z\) であり、等しくなります。
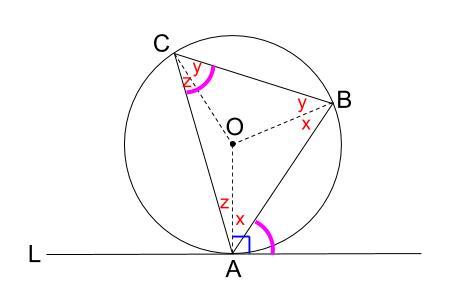
左側の角も同様に示せます。
例題1
下の図において、
\(AB=10cm\) の長方形が円に内接している。
\(BAE=60°\) のとき、この円の面積を求めなさい。
ただし、直線 \(E\) は円の接線、 \(A\) は接点である。
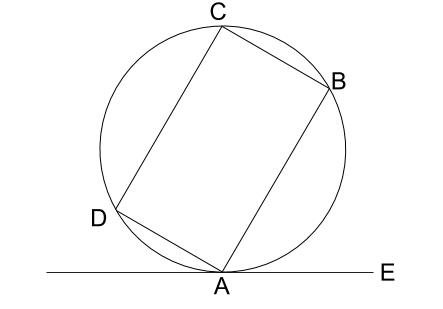
解説
接弦定理を知らなくとも解けます。
角 \(DAB\) が直角なので、\(BD\) は円の直径です。中心を \(O\) とします。
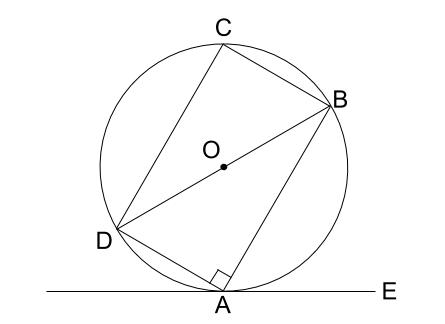
円の中心と接点を結ぶ補助線を引くのは定石ですね。
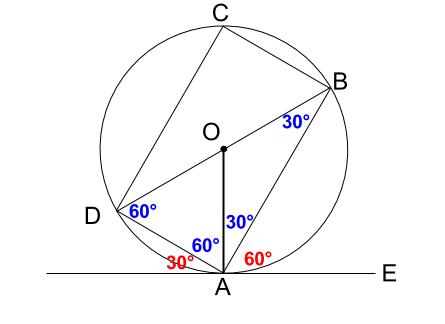
もし接弦定理を知っていれば、\(O\) から \(A\) への補助線なしで、解決します。
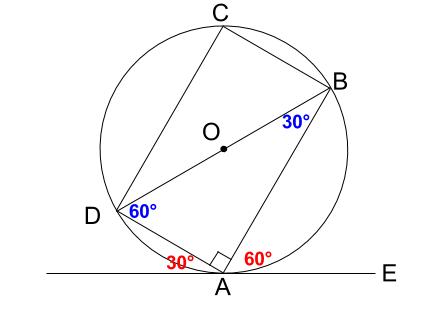
よって、三角形 \(BDA\) は、正三角形を半分にした三角定規型の有名三角形です。
\(AB=10cm\) から、\(AD=10×\displaystyle \frac{1}{\sqrt{3}}=\displaystyle \frac{10\sqrt{3}}{3}\)
\(AD\) の長さは、円の半径と等しいので、この円の面積は
\(\pi(\displaystyle \frac{10\sqrt{3}}{3})^2=\displaystyle \frac{100}{3}\pi\)