三角形の決定

余弦定理のページで、「正弦定理」でも「余弦定理」でも解けてしまう問題を見ました。

すべての問題が、「正弦定理」でも「余弦定理」でも解けるのかというと、そんなことはありません。

どちらか片方しか使えない問題もたくさんあります。

結局どのような問題のときに、どっちを使えばいいのか？
という「正弦定理」と「余弦定理」の使い分けが重要だということなのです。

外接円の半径の話がでてきたら間違いなく「正弦定理」なので、
このページではこのタイプの問題は除外します。

まずは例題を見て考えてみてください。
「正弦定理」と「余弦定理」、どちらを使えば答えがでる問題なのでしょう？

例題

次のような三角形 \(ABC\) において、指定されたものを求めなさい。

（１）\(b=6,B=30°,C=15°\) のとき、長さ \(a\) を求めよ。

（２）\(A=60°,a=\sqrt{6},b=2\sqrt{2}\) のとき \(c\) を求めよ。

（３）\(a=5,b=2\sqrt{3},A=30°\) のとき、長さ \(c\) を求めよ。

解説

なんとなくうまく解ける、という人も多いと思います。
解けるならそれはそれでＯＫなんですけど（筆者も高校生のときはなんとなく解いていました）、

「正弦定理」と「余弦定理」の使い分けのコツはあるんです。

せっかくこのページを見てるんですから、覚えていってくださいな。

このやり方はもっともオススメするものです。
ただし、「向かい合う角と辺がある」問題なのに、正弦定理では解けない問題があります。
そのときは余弦定理で解いてください。

やり直しの可能性があるというデメリットですが、
「絶対にやり直しをしなくてよい解き方」をマスターする労力に比べれば、たいした手間ではありません。

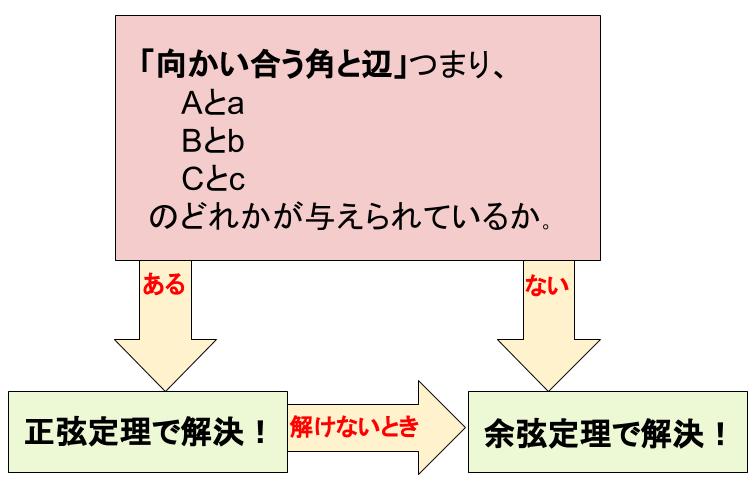
もちろん、向かいあう角と辺は、同じアルファベットです。
角が大文字で辺が小文字ですね！

では例題を解いていきましょう。

（１）\(b=6,B=30°,C=15°\) のとき、長さ \(a\) を求めよ。

向かい合う角と辺があるかどうかを見ます。
\(b\) と \(B\) があります。
よって、正弦定理を用いましょう。

長さ \(a\) を求めたいのですから、角 \(A\) がないといけません。
三角形の内角から容易に、 \(A=135°\) がわかります。

\(\displaystyle \frac{a}{\sin A}=\displaystyle \frac{b}{\sin B}\)

に代入して、

\(\displaystyle \frac{a}{\sin 135°}=\displaystyle \frac{6}{\sin 30°}\)

よって、\(a=6\sqrt{2}\)

あっさり解けましたね！

ちなみにこの問題を余弦定理で解くことはできません。

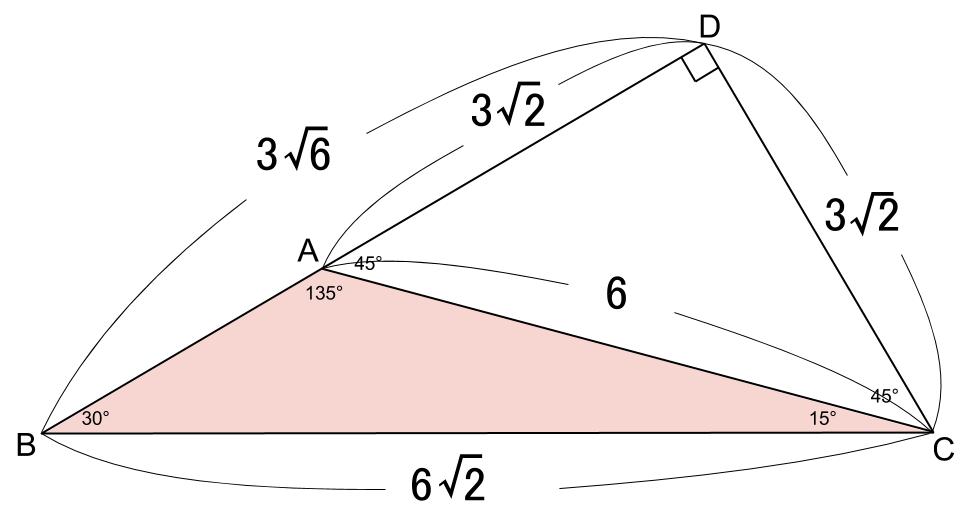
また、有名角が \(2\) つあるので、図示することで解決することもできます。
下図のように延長して、点 \(D\) をとります。
この作図をすれば、 \(c=3\sqrt{6}-3\sqrt{2}\) であることも求まります。

（２）\(A=60°,a=\sqrt{6},b=2\sqrt{2}\) のとき \(c\) を求めよ。

この問題も、向かい合う角と辺があるので、正弦定理です！
\(a\) と \(A\) ですね。

\(\displaystyle \frac{\sqrt{6}}{\sin 60°}=\displaystyle \frac{2\sqrt{2}}{\sin B}\)

これを解いて
\(\sin B=1\)
より、
\(B=90°\)
三角形の内角より、\(C=30°\)

今回の三角形 \(ABC\) の内角は、\(30°,60°,90°\)　となることが判明しました。

\(c\) の長さは、図示しても求まるし、正弦定理をもう \(1\) 回使っても求まります。
正弦定理で解くと

\(\displaystyle \frac{c}{\sin 30°}=2\sqrt{2}\)

より、\(c=\sqrt{2}\) です。

ちなみにこの問題は、余弦定理で解くことも可能です。
余弦定理で解くならば、与えられた角 \(A\) の向かいの辺 \(a\) からはじまる式です。
\(a^2=b^2+c^2-2bc\cos A\) に代入して、
\((\sqrt{6})^2=(2\sqrt{2})^2+c^2-2\cdot2\sqrt{2}c\cdot\displaystyle \frac{1}{2}\)

整理すると、\(c^2-2\sqrt{2}c+2=0\)
\((c-\sqrt{2})^2=0\)
より、\(c=\sqrt{2}\) です。

余弦定理は \(2\) 次方程式を解くことになることが多く、問題の数値設定しだいで、計算はやや面倒です。
どちらでも解ける問題においては、やはり「正弦定理」を利用したいものです。

（３）\(a=5,b=2\sqrt{3},A=30°\) のとき、長さ \(c\) を求めよ。

この問題も、向かい合う角と辺があるので、正弦定理です！
\(a\) と \(A\) ですね。

\(\displaystyle \frac{5}{\sin 30°}=\displaystyle \frac{2\sqrt{3}}{\sin B}\)

\(\sin B=\displaystyle \frac{\sqrt{3}}{5} \)

あ、これは \(B\) が有名角ではないですね・・・

これでは \(B\) が求まりません。

これが、おススメ方式の唯一の弱点、やり直しの必要があるタイプです。

このようなときは、「余弦定理」で解きます。
もし \(B,C\) が有名角ならば、「正弦定理」だけで済ませることができたのですが。
今回は「余弦定理」を使うしかありません。

分かっている角が \(A\) なので、向かいの辺 \(a\) からはじまる式を使います。

\(5^2=(2\sqrt{3})^2+c^2-2×2\sqrt{3}×c×\cos 30°\)

あとはこれを整理すると
\(25=12+c^2-6c\)

\(c^2-6c-13=0\)
この \(2\) 次方程式を解いて

\(c=3 \pm \sqrt{22}\)

\(c\) は \(0\) より大きいので、
\(c=3+\sqrt{22}\)

長くなってきました。
例題をあと \(2\) つ、次のページにて学習しましょう。