三角関数がはじまるよ！

このページから、「三角関数」がはじまります。

現代社会において、ありとあらゆる分野で大活躍する「三角関数」です。

ゲーム開発や音楽にも実用的応用がある「三角関数」です。

高校数学において、その「実用的応用」に触れることはありませんが、
現代社会を支える数学の基礎の基礎に慣れ親しんでおきましょう。

三角関数の定義

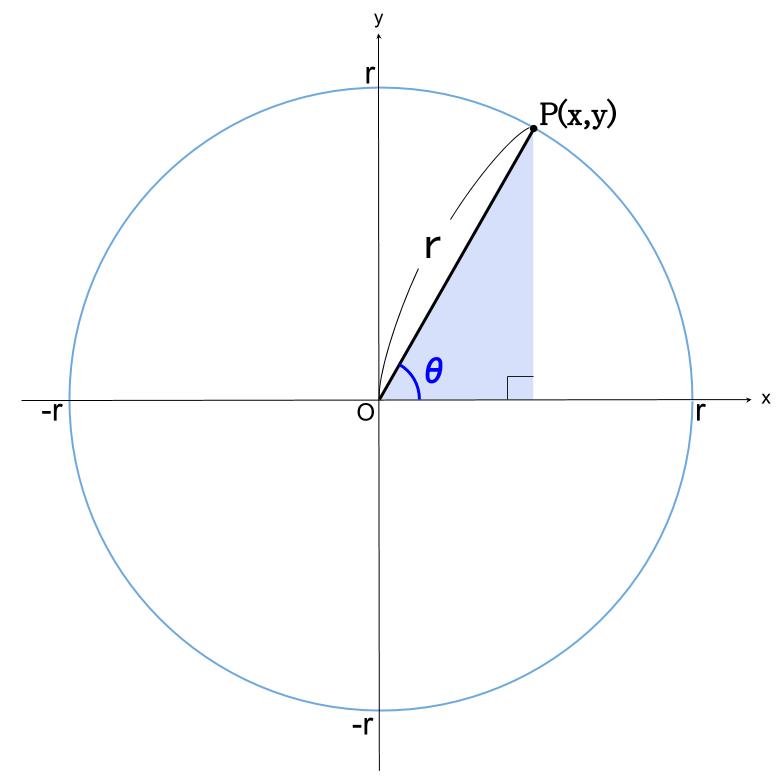
\(x\) 軸の正の部分を始線とし、角 \(\theta\) の動径 \(OP\) と
半径 \(r\) の円との交点を \(P(x,y)\) とするとき
以下のように定義する。

\(\sin \theta=\displaystyle \frac{y}{r}\)

\(\cos \theta=\displaystyle \frac{x}{r}\)

\(\tan \theta=\displaystyle \frac{y}{x}\)

ただし、\(\tan \theta\) は \(x=0\) となる角 \(\theta\) では定義されません

\(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\) は \(\theta\) の関数で、
これらを三角関数といいます。

数学Ⅰで学んだ「三角比」と何ら変わらないですね。

そうなんです、まったく同じと思ってもらって結構です。

角 \(\theta\) が一般角であることが違いなのですが、特別意識するようなことでもありません。

単位円による三角関数の定義

上の話において、 \(r=1\) の場合を考えます。
半径 \(1\) の円を単位円といいます。

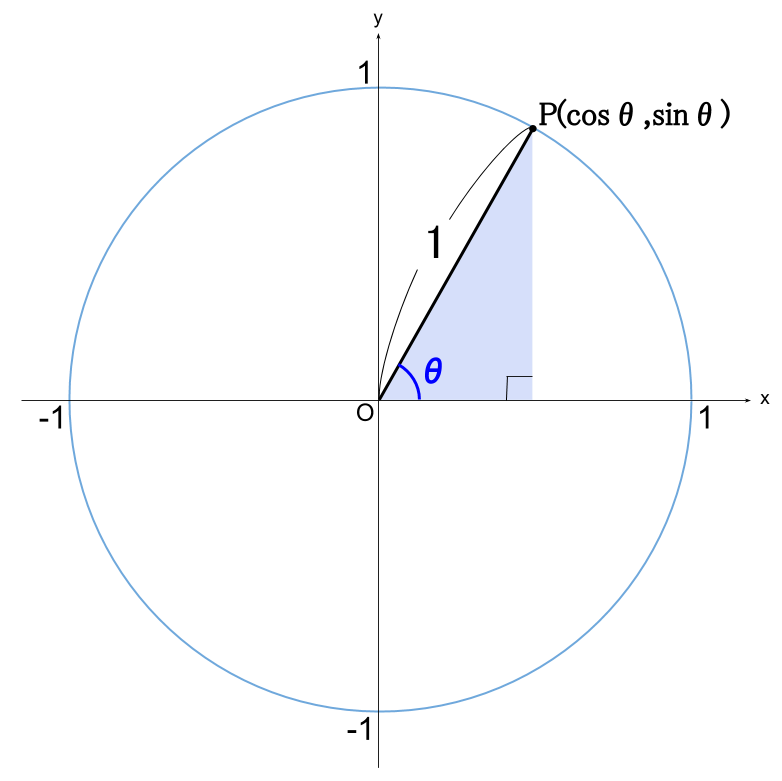
先ほどの三角関数の定義において、 \(r=1\) とすると

\(\sin \theta=\displaystyle \frac{y}{1}=y\)

\(\cos \theta=\displaystyle \frac{x}{1}=x\)

つまり、

\(\sin \theta\) は点 \(P\) の \(y\) 座標

\(\cos \theta\) は点 \(P\) の \(x\) 座標

となります。

\(\tan \theta=\displaystyle \frac{y}{x}\) なので、直線 \(OP\) の傾きです。

この話も数学Ⅰで学習したとおりです！
同じです！

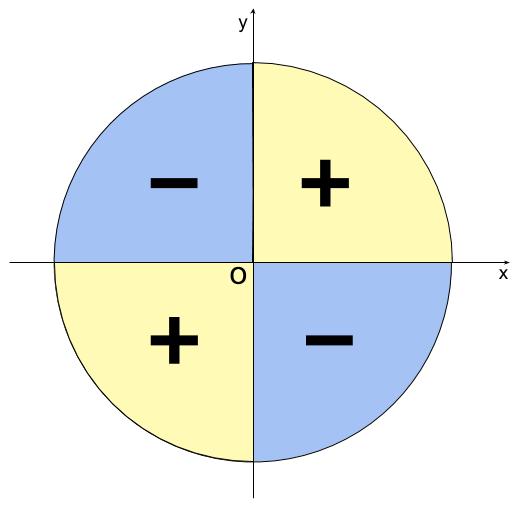
三角関数の符号と、とりうる値

\(\sin \theta\)の符号と、とりうる値

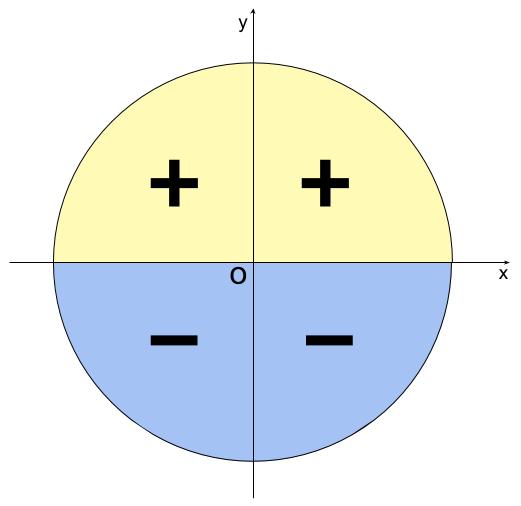
\(\sin \theta\) は単位円周上の点 \(P\) の \(y\) 座標です。
\(-1 \leqq \sin \theta \leqq 1\)

\(\cos \theta\)の符号と、とりうる値

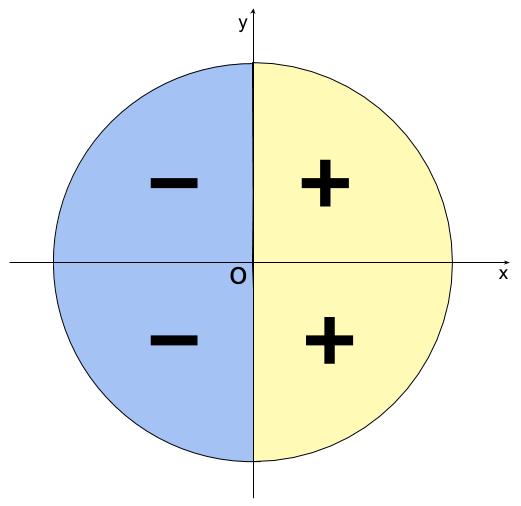
\(\cos \theta\) は単位円周上の点 \(P\) の \(x\) 座標です。
\(-1 \leqq \cos \theta \leqq 1\)

\(\tan \theta\)の符号と、とりうる値

\(\tan \theta=\displaystyle \frac{y}{x}\) なので、直線 \(OP\) の傾きです。
\(\tan \theta\) は実数全体をとる。

例題１

\(\theta=-240°\) のとき、\(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\)
をそれぞれ求めなさい。

解答

単位円を図示して考えます。
水色の直角三角形が有名三角形で、辺の比を暗記ですね。

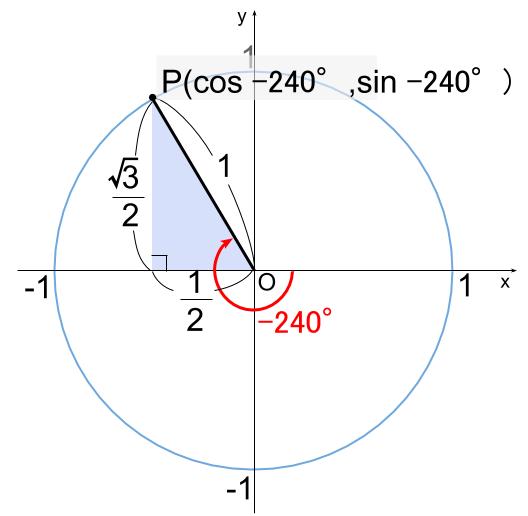
つまり、\(-240°\) と \(120°\) は動径の位置が同じです。

\(\sin -240°=\displaystyle \frac{\sqrt{3}}{2} \)

\(\cos -240°=-\displaystyle \frac{1}{2} \)

\(\tan -240°=-\sqrt{3} \)

例題２

\(\theta=\displaystyle \frac{7}{4} \pi \) のとき、\(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\)
をそれぞれ求めなさい。

解答

数学Ⅰで学習した三角比と結局は同じなんですけど、
最大の違いは「弧度法」で表示されるということです。

「三角関数」は「度数法」で定義したって本質的なことは何も変わりません。
度数法で表示しても何の問題もないのですが、
「弧度法」で学習していくのが数学Ⅱと思ってください。

単位円を図示して考えます。
水色の直角三角形が有名三角形で、辺の比を暗記ですね。

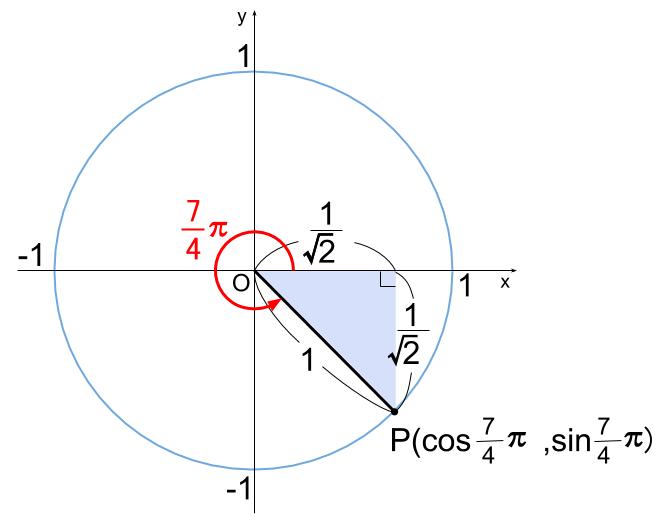
\(\sin \displaystyle \frac{7}{4} \pi =-\displaystyle \frac{1}{\sqrt{2}} \)

\(\cos \displaystyle \frac{7}{4} \pi =\displaystyle \frac{1}{\sqrt{2}} \)

\(\tan \displaystyle \frac{7}{4} \pi =-1\)