ポイント

\(\sin 2\theta(\cos 2\theta)\) と \(\sin \theta(\cos \theta)\) が混在している式は、
\(2\) 倍角の公式を用いて、角を \(\theta\) にそろえることをまず考えます。
そのような式変形をすれば、おのずと活路が見えてくる、そんな問題が出題されます。

角が \(\theta\) にそろったとき、\(\sin \theta\) と \(\cos \theta\) がある式は、合成をします。

例題１

関数 \(y=\sqrt{2} \sin \theta-\sqrt{6}\cos \theta\) の最大値、最小値を求めなさい。
また、そのときの \(\theta\) を求めなさい。\((0 \leqq \theta \lt 2\pi)\)

解説

\(\sin \theta\) と \(\cos \theta\) が同じ角のときは、合成します。

\(y=2\sqrt{2} \sin (\theta+\displaystyle \frac{5}{3}\pi)\)

\(\theta+\displaystyle \frac{5}{3}\pi=\displaystyle \frac{\pi}{2}+2n\pi\) のとき、最大値 \(2\sqrt{2}\)　をとり、

\(\theta+\displaystyle \frac{5}{3}\pi=\displaystyle \frac{3}{2}\pi+2n\pi\) のとき、最小値 \(-2\sqrt{2}\)　をとる。

よって、\(0 \leqq \theta \lt 2\pi\) のとき

\(\theta=\displaystyle \frac{5}{6}\pi\) で最大値 \(2\sqrt{2}\)

\(\theta=\displaystyle \frac{11}{6}\pi\) で最小値 \(-2\sqrt{2}\)

例題２

関数 \(y=2 \sin \theta -\cos 2\theta\) の最大値と最小値を求めなさい。
また、そのときの \(\theta\) を求めなさい。\((0 \leqq \theta \lt 2\pi)\)

解説

\(2\) 倍角の公式を用います。

\(\cos 2\theta=1-2 \sin^2 \theta\)

を用いれば

\(y=2 \sin \theta -(1-2 \sin^2 \theta)\)

\(y=2 \sin^2 \theta + 2 \sin \theta -1\)・・・①

\(\sin \theta=t\) とおくと　\(-1 \leqq t \leqq 1\)
①は、
\(y=2t^2+2t-1\)
平方完成すると

\(y=2(t+ \displaystyle \frac{1}{2})^2- \displaystyle \frac{3}{2}\)
\(-1 \leqq t \leqq 1\) で下図のようになります。

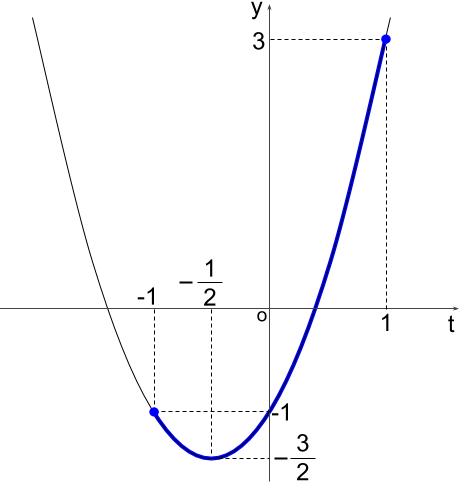
より、\(t=-\displaystyle \frac{1}{2}\) のとき、最小値 \(-\displaystyle \frac{3}{2}\)

つまり、
\(\sin \theta=-\displaystyle \frac{1}{2}\) のときなので、\(\theta=\displaystyle \frac{7}{6}\pi,\displaystyle \frac{11}{6}\pi\) のとき、最小値 \(-\displaystyle \frac{3}{2}\)

\(t=1\) のとき、最大値 \(3\)
つまり、
\(\sin \theta=1\) のときなので、\(\theta=\displaystyle \frac{\pi}{2}\) のとき、最大値 \(3\)

例題３

\( \displaystyle \frac{\pi}{2} \leqq \theta \leqq \pi\) のとき、次の関数の最大値と最小値を求めよ。
\(y=\sin 2\theta+\cos 2\theta+1\)
また、そのときの \(\theta\) を求めなさい。

解説

\(2\theta\) だから \(2\) 倍角？
いいえ、合成ですよ！！
\(y=\sin 2\theta+\cos 2\theta+1\) の \(\sin 2\theta+\cos 2\theta\) の合成をすると

\(y=\sqrt{2}\sin (2\theta+\displaystyle \frac{\pi}{4})+1\)・・・①

\( \displaystyle \frac{\pi}{2} \leqq \theta \leqq \pi\) なので、

\( \pi \leqq 2\theta \leqq 2\pi\)

\( \pi+\displaystyle \frac{\pi}{4} \leqq 2\theta+\displaystyle \frac{\pi}{4} \leqq 2\pi+\displaystyle \frac{\pi}{4}\)

\( \displaystyle \frac{5}{4}\pi \leqq 2\theta+\displaystyle \frac{\pi}{4} \leqq \displaystyle \frac{9}{4}\pi\)

この範囲で、\(\sin (2\theta+\displaystyle \frac{\pi}{4})\) のとる値は下図のようになります。

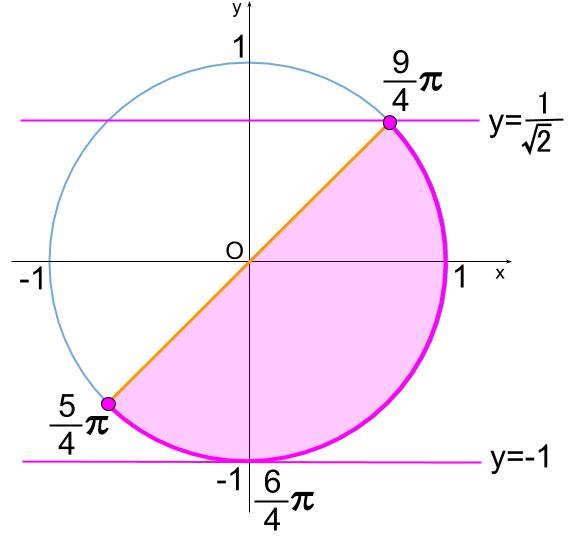
よって、\(\sin (2\theta+\displaystyle \frac{\pi}{4})=\sin \displaystyle \frac{9}{4}\pi\) のとき、

\(\sin (2\theta+\displaystyle \frac{\pi}{4})\) は最大値 \(\displaystyle \frac{1}{\sqrt{2}}\) をとる。

つまり、\(\theta=\pi\) のときに、

\(y=\sqrt{2}\sin (2\theta+\displaystyle \frac{\pi}{4})+1=\sqrt{2}×\displaystyle \frac{1}{\sqrt{2}}+1=2\)　より、最大値 \(2\)

また、\(\sin (2\theta+\displaystyle \frac{\pi}{4})=\sin \displaystyle \frac{6}{4}\pi\) のとき、

\(\sin (2\theta+\displaystyle \frac{\pi}{4})\) は最小値 \(-1\) をとる。

つまり、\(\theta=\displaystyle \frac{5}{8}\pi\) のときに、

\(y=\sqrt{2}\sin (2\theta+\displaystyle \frac{\pi}{4})+1=\sqrt{2}×(-1)+1=1-\sqrt{2}\)　より、最小値 \(1-\sqrt{2}\)