連立不等式

連立不等式の解き方。

それぞれの不等式を解きます。
解の共通部分が、連立不等式の解となります。
それぞれの解を数直線上に表しましょう。

次の連立不等式を解きなさい。

$\begin{eqnarray} \left\{ \begin{array}{l} 4x+2 \leqq 3x-3 \\ -x-7 \lt x+9\ \end{array} \right.\end{eqnarray}$

それぞれの不等式を解き、解を数直線上に表します。
その共通範囲を求めます。

$4x+2 \leqq 3x-3$ を解くと、$x \leqq -5$・・・①

$-x-7 \lt x+9$ を解くと、$-8 \lt x$・・・②

①、②を数直線上に表すと

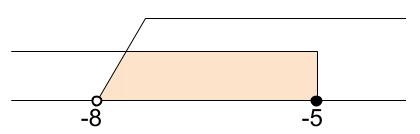
$高校数学無料学習サイトko-su- 連立不等式１$

よって、
$-8 \lt x \leqq -5$

次の連立不等式を解きなさい。
$-3x+1 \lt x \lt 2x-2$

$A \lt B \lt C$
は、連立不等式
$\begin{eqnarray} \left\{ \begin{array}{l} A \lt B\ \\ B \lt C \end{array} \right.\end{eqnarray}$
と同じことです。

つまり、
$\begin{eqnarray} \left\{ \begin{array}{l} -3x+1 \lt x\ \\ x \lt 2x-2 \end{array} \right.\end{eqnarray}$
を解きます。

$-3x+1 \lt x $ を解いて、$x \gt \displaystyle \frac{1}{4}$・・・①

$x \lt 2x-2$ を解いて、$x \gt 2$・・・②

①、②を数直線上に表すと

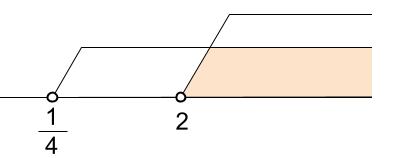
$高校数学無料学習サイトko-su- 連立不等式２$

よって、
$x \gt 2$

連立不等式
$\begin{eqnarray} \left\{ \begin{array}{l} -x+2 \gt -3x \\ x-a \leqq 0\ \end{array} \right.\end{eqnarray}$

を満たす整数 $x$ がちょうど $3$ 個存在するような定数 $a$ の値の範囲を求めなさい。

$ -x+2 \gt -3x$ を解いて、$x \gt -1$
$x-a \leqq 0$ を解いて、$x \leqq a$
共通部分を図示します。

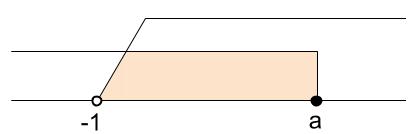
$高校数学無料学習サイトko-su- 連立不等式3-1$

この範囲に整数が $3$ 個なので、その $3$ 個の整数は $0,1,2$ となります。
$a$ も含めるので、最小の $a$ は $a=2$ のとき

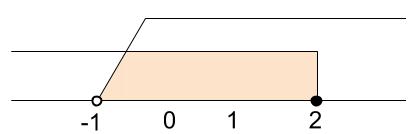
$高校数学無料学習サイトko-su- 連立不等式3-2$

最大の $a$ は $a=2.999\cdots$ のとき

$高校数学無料学習サイトko-su- 連立不等式3-3$

つまり、定数 $a$ の値の範囲は
$2 \leqq a \lt 3$