メネラウスの定理・最終奥義
メネラウスの定理はいらない!?最終奥義があるから
メネラウスの定理は、上手に適用することがなかなか難しいということを前ページで見ました。
そこで、
このページでは、チェバ・メネラウス・メネラウスの発展すべてを
統一的に扱う方法を伝授します。
それは、面積比による方法です。
1.下図のように三角形の面積比と、辺の長さの比が一致する。
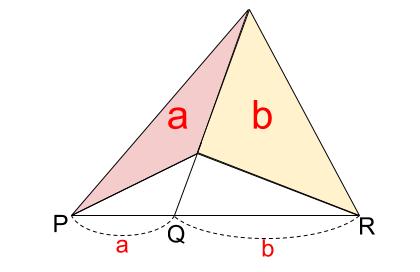
赤三角形の面積とクリーム色三角形の面積比が \(a:b\) なら、
\(PQ:QR=a:b\)
2.下図のように面積比と、辺の長さの比が一致する。
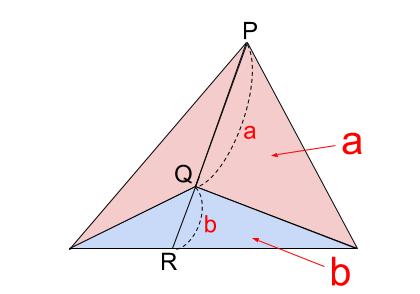
赤いブーメラン型の面積と水色三角形の面積比が \(a:b\) なら、
\(PQ:QR=a:b\)
この \(2\) つの性質を使えば、
普通の高校生がチェバの定理やメネラウスの定理を用いて解く問題を、
チェバの定理もメネラウスの定理も一切使用しないで解くことができます。
実際に例題で見ていきましょう。
前ページで、チェバの定理やメネラウスの定理を用いて解いた例題を、この方法を用いてどのように解くかを見ていきましょう。
例題1
下の図で、\(BQ:QC=3:5\)、\(AR:RC=7:8\) のとき、\(AP:PB\) を求めなさい。
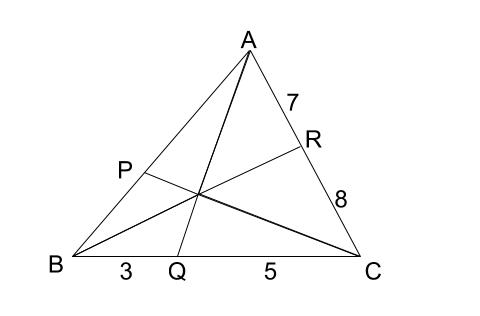
解説
これはチェバの定理でサクッと解けるのですが、面積比で解くと以下のようになります。
\(BQ:QC=3:5\) より、下図の面積比がわかります。
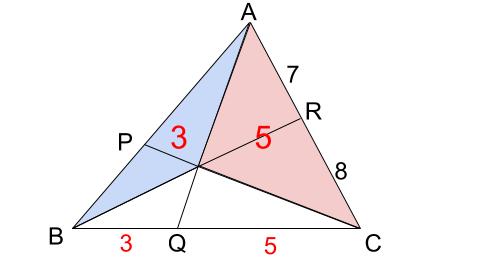
また、\(AR:RC=7:8\) より、下図の面積比がわかります。
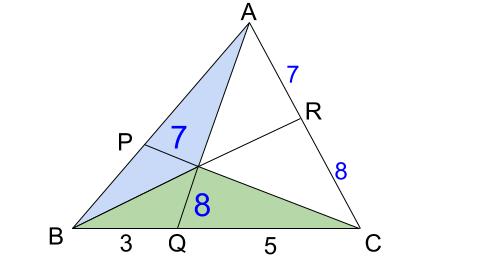
水色の三角形が \(2\) つの比で共通です。
\(3\) と \(7\) の最小公倍数 \(21\) でそろえると下図のようになります。
水色の三角形を \(ABD\) とします。
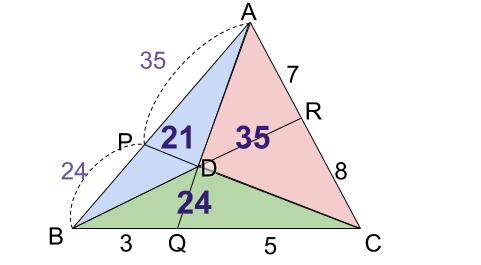
よって、
\(AP:PB=35:24\) です。
以上求まりました。
ちなみに、
\(AD:DQ=(21+35):24=56:24=7:3\)
\(BD:DR=(21+24):35=45:35=9:7\)
\(CD:DP=(24+35):21=59:21\)
あらゆる線分の比が求まります。
例題2
下の図で、\(AB:BC=3:2\)、\(CD:DF=6:5\) のとき、\(AF:FE\) を求めなさい。
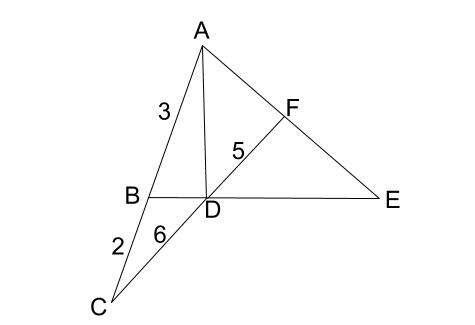
解説
多くの高校生がメネラウスの定理で解く問題ですが、これをメネラウスの定理なしで解きます。
まずは補助線を引いて、チェバの定理のときと同じような図形にします。
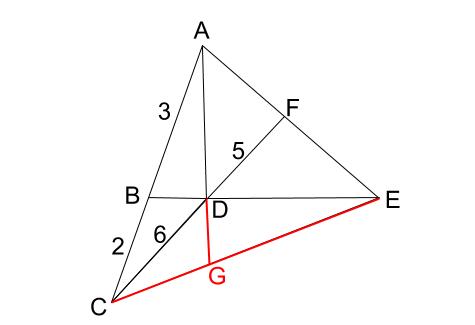
与えられた線分の比からわかる面積比は下図のようになります。
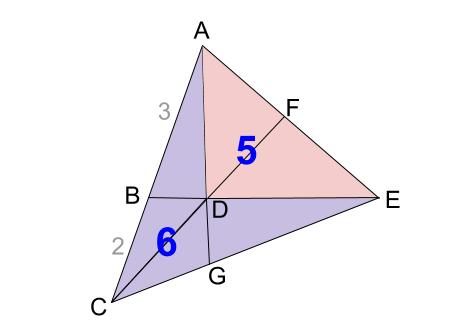
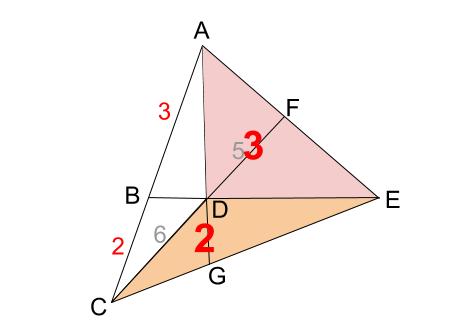
ピンク色の三角形 \(ADE\) が \(2\) つの比で共通です。
\(5\) と \(3\) の最小公倍数 \(15\) でそろえると下図のようになります。
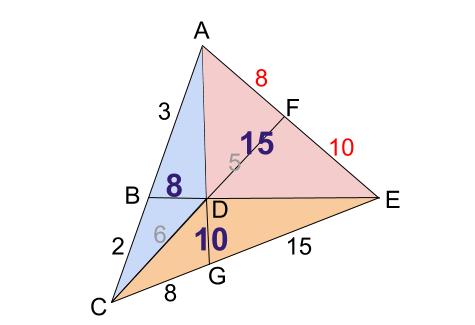
よって、
\(AF:FE=8:10=4:5\) です。
以上求まりました。
メネラウスの定理を適用するとき特有の難しさがないことがお分かりいただけると思います。図の中で、どれが三角形で、どれが直線なのかを見極める必要がまったくありません。