順列と確率
順列と確率
基本的に確率は、「場合の数」を求めることに終始します。
適切に場合の数を求められるように、必要ならば「場合の数」の単元を読み返しましょう。
例題1
男子 \(4\) 人と女子 \(3\) 人が \(1\) 列に並ぶとき、次の確率を求めなさい。
(1)女子 \(3\) 人が続いて並ぶ
(2)両端が男子である
(3)男女が交互に並ぶ
解説
何の条件もない \(7\) 人の並び方の総数を分母とし、それぞれ「条件を満たす場合の数」を分子として、確率を求めます。
全問題に共通の分母を求めておきます。
\(7\) 人が一列に並ぶ並び方の総数は、
\(7!\) 通りです。
(1)女子 \(3\) 人が続いて並ぶ
女子 \(3\) 人を一かたまりとすれば、
男子 \(4\) 人と、女子のかたまり \(1\) つの、合計 \(5\) つのものの順列なので、\(5!\) 通り。
さらに、女子は、一かたまりの中で並べ替えがあるので、\(3\) 人の順列で \(3!\) 通り
よって、女子 \(3\) 人が続いて並ぶ並び方の総数は、\(5!×3!\) 通り
よって求める確率は、
\(\displaystyle \frac{5!×3!}{7!}=\displaystyle \frac{5×4×3×2×1×3×2×1}{7×6×5×4×3×2×1}\)\(=\displaystyle \frac{3×2×1}{7×6}=\displaystyle \frac{1}{7}\)
以上求まりました。
(2)両端が男子である
左端と右端に \(2\) 人を並べます。男子 \(4\) 人から \(2\) 人を選んで並べるので、
\(_4 \mathrm{ P }_2\) 通り。
さらに、間に入る \(5\) 人の並べ方は、\(5\) 人の順列で \(5!\) 通り
よって、両端が男子である並び方の総数は、\(_4 \mathrm{ P }_2×5!\) 通り
よって求める確率は、
\(\displaystyle \frac{_4 \mathrm{ P }_2×5!}{7!}=\displaystyle \frac{4×3×5×4×3×2×1}{7×6×5×4×3×2×1}\)\(=\displaystyle \frac{4×3}{7×6}=\displaystyle \frac{2}{7}\)
(3)男女が交互に並ぶ
「男女男女男女男」と並ぶことになります。
男子 \(4\) 人は、\(4\) 人の順列で \(4!\) 通り
女子 \(3\) 人は、\(3\) 人の順列で \(3!\) 通り
よって、男女が交互に並ぶ並び方の総数は、\(4!×3!\) 通り
よって求める確率は、
\(\displaystyle \frac{4!×3!}{7!}=\displaystyle \frac{4×3×2×1×3×2×1}{7×6×5×4×3×2×1}\)\(=\displaystyle \frac{3×2×1}{7×6×5}=\displaystyle \frac{1}{35}\)
例題2
男子 \(4\) 人と女子 \(3\) 人が円形に並んで輪をつくるとき、次の確率を求めなさい。
(1)女子 \(3\) 人が続いて並ぶ
(2)女子が隣り合わない
解説
全問題に共通の分母を求めておきます。
\(7\) 人が円形に並ぶ円順列の総数は、
\((7-1)!\) 通りです。
(1)女子 \(3\) 人が続いて並ぶ
女子 \(3\) 人を一かたまりとすれば、
男子 \(4\) 人と、女子のかたまり \(1\) つの、合計 \(5\) つのものの円順列なので、\((5-1)!\) 通り。
さらに、女子は、一かたまりの中で並べ替えがあるので、\(3\) 人の順列で \(3!\) 通り
よって、女子 \(3\) 人が続いて並ぶ並び方の総数は、\((5-1)!×3!\) 通り
よって求める確率は、
\(\displaystyle \frac{(5-1)!×3!}{(7-1)!}=\displaystyle \frac{4×3×2×1×3×2×1}{6×5×4×3×2×1}\)\(=\displaystyle \frac{3×2×1}{6×5}=\displaystyle \frac{1}{5}\)
以上求まりました。
(2)女子が隣り合わない
ちょっと難しいです。
きちんと図示をして、頭の中を整理して、論理的に計算を進めましょう。
男子を円形に並べ、その間に \(1\) 人ずつ女子を入れます。
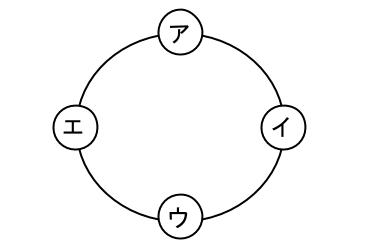
図示するために、男子にア、イ、ウ、エと名前をつけます。
男子 \(4\) 人の円順列は、\((4-1)!\) 通りあります。
その中の一例です。
女子 \(3\) 人を \(P,Q,R\) と名前をつけます。
この3人が、それぞれ下図の \(1,2,3,4\) のどこに入るかを決めます。
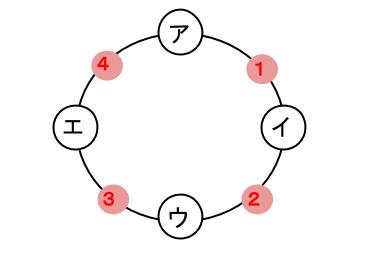
\(P\) が \(1\) 番に入るときのかき出しは下図です。
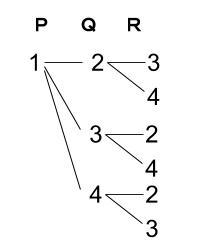
つまり、\(1,2,3,4\) から \(3\) つを選んで並べる順列であることがわかりました。
つまり、\(_4 \mathrm{ P }_3\) 通り。
以上合わせて、女子が隣り合わない並び方は、
\((4-1)!×_4 \mathrm{ P }_3\) 通り。
よって、求める確率は、
\(\displaystyle \frac{(4-1)!×_4 \mathrm{ P }_3}{(7-1)!}\)\(=\displaystyle \frac{3×2×1×4×3×2}{6×5×4×3×2×1}=\displaystyle \frac{1}{5}\)
以上求まりました。