確率をかけ算するとき・確率の乗法定理
独立な試行でない確率をかけ算する
確率どうしを足し算することや、確率どうしをかけ算するケースを見てきました。
排反事象の確率を足し算したり、独立な試行の確率をかけ算してきました。
それ以外の重要なケースを学習します。
例題1
赤球 \(3\) 個、白球 \(2\) 個の入った袋から、\(1\) 個ずつ球を \(2\) 個取り出します。
取り出した球はもとに戻しません。
\(1\) 個目の球の色が白で、\(2\) 個目の球の色が赤となる確率を求めなさい。
解説
\(2\) 回の試行は互いに独立ではありませんね。
\(1\) 回目に取り出した球の色によって、\(2\) 回目の試行の確率が変動するからです。
つまり、\(1\) 回目と \(2\) 回目の試行は繋がっています。
このように、独立でない試行の確率がどうなるか、これがこのページのテーマです。
赤球 1,2,3
白球 ア、イ
と名付けます。
ではまず、樹形図による全書き出しで答えを求めます。
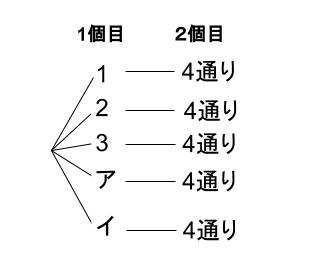
全取り出し方が \(5×4=20\)通りです。
\(1\) 個目の球の色が白のときだけ、\(2\) 個目の球も書き出してみます。
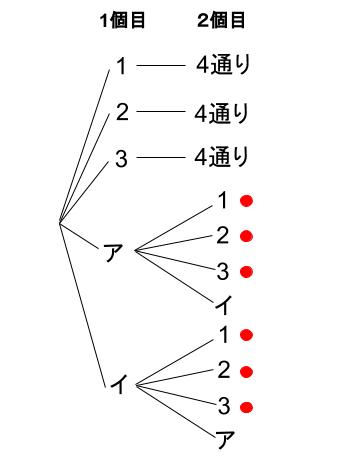
\(1\) 個目の球の色が白で、\(2\) 個目の球の色が赤である取り出し方は、
印のついた \(6\) 通りです。
全取り出し方が \(5×4=20\)通りなので、求める確率は、
\(\displaystyle \frac{6}{20}=\displaystyle \frac{3}{10}\) です。
以上求まりましたが、これは以下のように、より簡単に求めることができます。
確率の積で求まる!
\(1\) 個目の球の色が白になる確率は、 \(\displaystyle \frac{2}{5}\) です。
全 \(5\) 個の中に、白球が \(2\) 個なので、当然です。
この \(\displaystyle \frac{2}{5}\) は、最終的に \(20\) 通りある取り出し方のうち、
\(20×\displaystyle \frac{2}{5}=8\) 通りに絞られたことを意味しています。
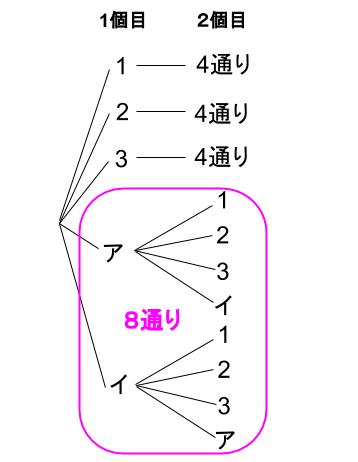
次に \(2\) 個目です。
このとき、袋の中には、赤球 \(3\) 個、白球 \(1\) 個が残っています。
この状態の袋から、赤球を取り出す確率は、 \(\displaystyle \frac{3}{4}\) です。
よって、\(1\) 個目の球の色が白で、\(2\) 個目の球の色が赤である取り出し方は、\(8×\displaystyle \frac{3}{4}=6\) 通り であることを意味しています。
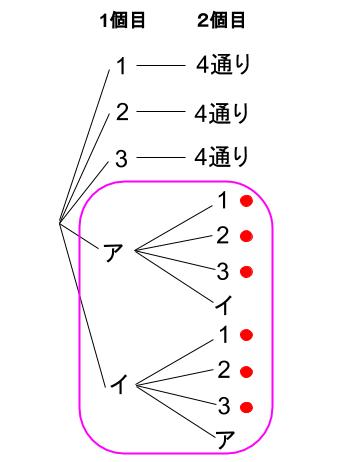
つまり、全 \(20\) 通りのうち、その \(\displaystyle \frac{2}{5}\) が該当し、さらにその中の \(\displaystyle \frac{3}{4}\) が該当するので、
全 \(20\) 通りの \(\displaystyle \frac{2}{5}×\displaystyle \frac{3}{4}=\displaystyle \frac{3}{10}\) 、\(20×\displaystyle \frac{2}{5}×\displaystyle \frac{3}{4}=6\) 通りが該当します。
それが起こる確率は、
\( \displaystyle \frac{20×\frac{2}{5}×\frac{3}{4}}{20}=\displaystyle \frac{2}{5}×\displaystyle \frac{3}{4}=\displaystyle \frac{3}{10}\)
つまり、確率の積となります!
\(1\) 回目と \(2\) 回目は独立な試行ではありませんが、ともに起こる確率は、確率の積で求まります。
樹形図から明らかですね。
独立な試行の確率の積と同じこと
ちょっと見方を変えて次の問題を考えてみましょう。
赤球 \(3\) 個、白球 \(2\) 個の入った袋 \(A\) から、\(1\) 個球を取りだします。
次に、
赤球 \(3\) 個、白球 \(1\) 個の入った袋 \(B\) から、\(1\) 個球を取りだします。
\(A\) から取り出した球の色が白で、\(B\) から取り出した球の色が赤となる確率を求めなさい。
答え
\(2\) 回の取り出しは独立な試行ですね。
よって、
\( \displaystyle \frac{2}{5}×\displaystyle \frac{3}{4}=×\displaystyle \frac{3}{10}\)
と求まります。
これって・・・先ほどの例題の取り出しとまったく同じ状況ですね。袋 \(B\) は「例題1の \(1\) 個白球を取り出した状態」とまったく同じだからです。
同じような計算で答えが出るに決まっています。
まとめ
結局どんなときに確率の積なのか?
独立か独立でないのかという区別は必要なのか?
樹形図による理解をきちんとしていれば、一切考慮しなくてOKです。
そして、
理解を伴わない言葉の暗記をしても使い物にならないので、結局不要です。
最も根源的で大切なことは、樹形図による場合の数の練習をきちんと積んでおくことです。
ここさえしっかりしていれば、確率の計算は、感覚的に行えるようになります。
例題2
赤球 \(5\) 個、白球 \(3\) 個の入った袋から、\(1\) 個ずつ球を \(2\) 個取り出します。
取り出した球はもとに戻しません。
\(2\) 個目の球の色が赤となる確率を求めなさい。
解説
(赤、赤)と取り出す確率と
(白、赤)と取り出す確率の和になります。
(赤、赤)の確率
\(1\) 個目に赤の確率は、\(\displaystyle \frac{5}{8}\)
次に、袋の中は、赤球 \(4\) 個、白球 \(3\) 個となっているので、
\(2\) 個目に赤の確率は、\(\displaystyle \frac{4}{7}\)
より、赤、赤と取り出す確率は、
\(\displaystyle \frac{5}{8}×\displaystyle \frac{4}{7}=\displaystyle \frac{5}{14}\)
(白、赤)の確率
\(1\) 個目に白の確率は、\(\displaystyle \frac{3}{8}\)
次に、袋の中は、赤球 \(5\) 個、白球 \(2\) 個となっているので、
\(2\) 個目に赤の確率は、\(\displaystyle \frac{5}{7}\)
より、白、赤と取り出す確率は、
\(\displaystyle \frac{3}{8}×\displaystyle \frac{5}{7}=\displaystyle \frac{15}{56}\)
よって、求める確率は、
\(\displaystyle \frac{5}{14}+\displaystyle \frac{15}{56}=\displaystyle \frac{35}{56}=\displaystyle \frac{5}{8}\)
※実は、何個目であっても、それが赤球である確率はすべて \(\displaystyle \frac{5}{8}\) です。
参考・確率の乗法定理
上で見てきた確率の積ですが、無駄に難しい言葉では、確率の乗法定理といいます。
条件付き確率という話からでてくるのですが、基本的には無視してもらってOKです。