数を並べる

例題１

\(1,2,3,4,5\) の \(5\) つの数字から \(3\) つを使い、 \(3\) 桁の数をつくります。同じ数字を \(2\) 回以上使うことはできません。次のような数は何通りつくれますか。

（１）奇数
（２）\(300\) 以下の数

解説

（１）奇数

奇数という条件から先に決めていきます。
奇数は、\(1\) の位が奇数ならばよいので、
\(1\) の位が、\(1,3,5\) のどれかになればＯＫです。

\(1\) の位が \(1\) のとき、百の位は \(4\) 通り、十の位は \(3\) 通りなので、
\(4×3=12\) 通りあります。

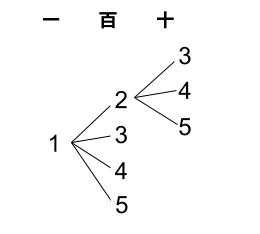
\(1\) の位が、\(3,5\) のときも同様に \(12\) 通りずつあるので、
全部で、\(3×12=36\) 通りです。

（２）300以下の数

百の位が、\(1,2\) ならば、条件を満たします。

百の位が \(1\) のとき、十の位は \(4\) 通り、一の位は \(3\) 通りなので、
\(4×3=12\) 通りあります。

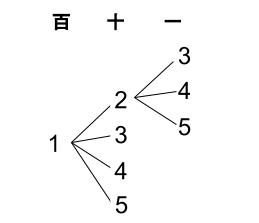
百の位が \(2\) のときも同様に \(12\) 通りあるので、
\(2×12=24\) 通りです

例題２

\(0,1,2,3,4,5\) の \(6\) つの数字から \(3\) つを使い、 \(3\) 桁の数をつくります。同じ数字を \(2\) 回以上使うことはできません。次のような数は何通りつくれますか。

（１）奇数
（２）偶数

解説

\(0\) が、最高位（今回は百の位）には使えないということが暗黙の条件となっています。
気をつけましょう！

（１）奇数

奇数は \(1\) の位が奇数です。
よって、\(1,3,5\) の \(3\) 通りです。

例えば \(1\) の位に \(1\) を使った場合

百の位は、\(2,3,4,5\) の \(4\) 通り
さらに、 百の位に \(2\) を使った場合、
十の位は、\(0,3,4,5\) の \(4\) 通り
よって、\(4×4=16\) 通りです。

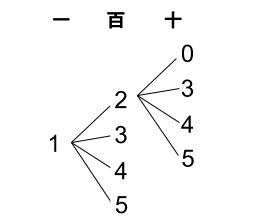
\(1\) の位に \(3,5\) を使った場合も同様に \(16\) 通りずつあるので、

\(3×16=48\) 通り

（２）偶数

偶数は \(1\) の位が偶数です。
よって、\(0,2,4\) の \(3\) 通りです。

\(1\) の位に \(0\) を使った場合

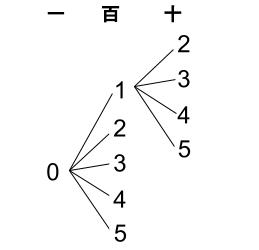
百の位は、\(1,2,3,4,5\) の \(5\) 通り
さらに、 百の位に \(1\) を使った場合、
十の位は、\(2,3,4,5\) の \(4\) 通り
よって、\(5×4=20\) 通りです。

\(1\) の位に \(2,4\) を使った場合も同様に \(20\) 通りずつあるのか・・・
いいえ。同様とは言えません。

\(0\) と \(2,4\) では条件が違います。
改めて調べるのです。

\(1\) の位に \(2,4\) を使った場合

\(1\) の位に \(2\) を使った場合

百の位は、\(1,3,4,5\) の \(4\) 通り（\(0\) は使えない！）
さらに、 百の位に \(1\) を使った場合、
十の位は、\(0,3,4,5\) の \(4\) 通り
よって、\(4×4=16\) 通り

\(1\) の位に \(4\) を使った場合も同様に \(16\) 通りあるので、

\(16×2=32\) 通りです。

よって、\(20+32=52\) 通り

別解

（全通り）－（奇数の場合）＝（偶数の場合）
が成り立ちます。余事象の考え方です。

\(3\) 桁の数は全部で、
百の位に、\(1,2,3,4,5\) の \(5\) 通り
もし、百の位に \(1\) を使った場合、
十の位は、\(0,2,3,4,5\) の \(5\) 通り
もし、十の位に \(0\) を使った場合、
一の位は、\(2,3,4,5\) の \(4\) 通り
つまり、\(5×5×4=100\) 通りです。

奇数は、（１）で\(48\) 通りと求めています。

よって、\(100-48=52\) 通り

例題３

\(1,2,3,4,5\) の \(5\) つの数字から \(3\) つを使い、 \(3\) 桁の数をつくります。同じ数字を \(2\) 回以上使うことはできません。次のような数は何通りつくれますか。

（１）\(4\) の倍数
（２）\(3\) の倍数

解説

（１）\(4\) の倍数

\(4\) の倍数は、下 \(2\) 桁が \(4\) の倍数です。数の性質の重要知識です。暗記しておきましょう。なぜかというと、\(100\) が \(4\) の倍数だからなのです。
※本問とは無関係ですが、\(00,04,08\) も含みます。

よって、下 \(2\) 桁が \(4\) の倍数になるものをかき出します。

\(12,24,32,52\) です。
すべての場合で、百の位に \(3\) 通りずつの枝分かれがあるので、

\(4×3=12\) 通り
求まりました。

（２）\(3\) の倍数

\(3\) の倍数は、各位の和が \(3\) の倍数になります。重要知識です。

よって、各位の和が、 \(3,6,9,12,\cdots\) となるものをかき出します。

各位の和は、最小で、\(1+2+3=6\)、最大で \(5+4+3=12\) なので、
各位の和が、 \(6,9,12\) となるものをかき出せばＯＫです。

各位の和が６

使う数の組合わせは、
\((1,2,3)\) の \(1\) 通りです。
これを並び替えて、\(3×2×1=6\) 通りの \(3\) 桁の数ができます。

各位の和が９

使う数の組合わせは、
\((5,3,1)\)
\((4,3,2)\)
の \(2\) 通りです。
どちらも、並び替えて、\(3×2×1=6\) 通りの \(3\) 桁の数ができるので、
\(6×2=12\) 通り

各位の和が12

使う数の組合わせは、
\((5,4,3)\) の \(1\) 通りです。
これを並び替えて、\(3×2×1=6\) 通りの \(3\) 桁の数ができます。

以上より、\(6+12+6=24\) 通り