円順列

公式の意味を確認しておきましょう。

\(A,B,C,D\) の \(4\) 人が \(1\) 列に並ぶ並び方は、\(4!=24\) 通りですね。

次に、左端の人と右端の人が手をつないで円形になりましょう。

\(24\) 通りの円形の並び方ができるのでしょうか？

例を見てみましょう。

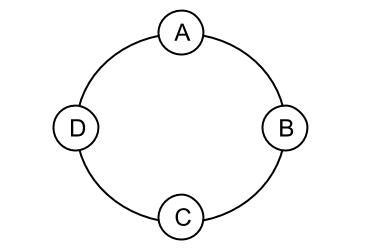
この円形は、\(A,B,C,D\) と並んだ後、\(A,D\) が手をつないだものです。

そして・・・

\(B,C,D,A\) と横一列に並んだ後、\(B,A\) が手をつないでも、上図の円形と同じ並び方になります。

同様に、
\(C,D,A,B\) が、円形に並んでも
\(D,A,B,C\) が、円形に並んでも
上図と同じ並び方になりますね。

つまり、\(4\) 通りの重複があります。
よって、
\(4!÷4=3!\) 通りになります。
これが円順列の総数です。

別の説明の仕方もあります。
まず \(A\) の位置を決めます。回転しても同じなので、\(A\) の位置は \(1\) 通りです。

残った \(3\) 箇所に、残りの \(3\) 人、\(B,C,D\) が並びます。
この並び方は、\(3!=6\) 通りです。

回転して同じになるものは \(1\) つと数えるため、順列を重複の数で割ったものが円順列なのです！

例題１

\(6\) 人が手をつないで輪をつくるとき、並び方は何通りありますか。

解説

公式一発で済ませましょう。
\((6-1)!=120\) 通りです。

例題２

夫婦 \(1\) 組と、その子ども \(4\) 人の合計 \(6\) 人が円卓に座るとき、次のような座り方は何通りありますか。
（１）夫婦が隣り合う
（２）夫婦が向い合う

解説

夫婦を \(A,B\) 、子どもをア、イ、ウ、エと名付けましょう。

（１）夫婦が隣り合う

条件から先に決めるのが場合の数の鉄則です。

夫婦 \(A,B\) を、一かたまりのものとして扱います。
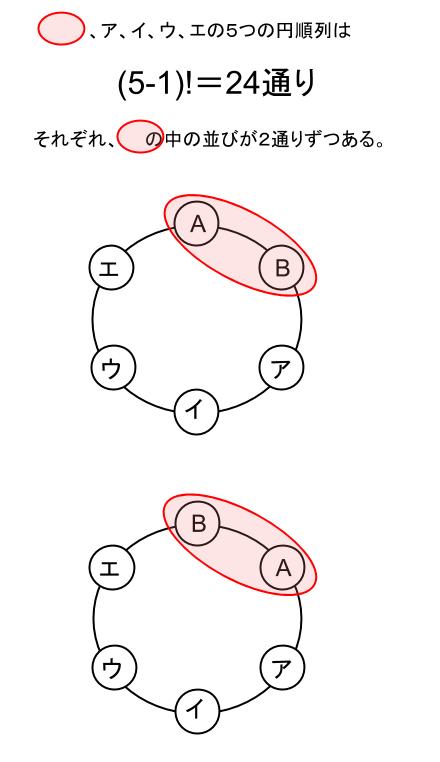
\((AB)\) と、子ども、ア、イ、ウ、エの \(5\) つのものの円順列です。
\((5-1)!=24\) 通りです。

夫婦は一かたまり \((AB)\) として並べていましたが、\((BA)\) と並べることもできるので、
\(24×2=48\) 通りです。

別解

まずは \(6\) 人を横一列に並べましょう。
夫婦 \(A,B\) を、一かたまりのものとして扱います。
\((AB)\) と、子ども、ア、イ、ウ、エの \(5\) つのものの順列です。

\(5!=120\) 通り

夫婦は一かたまり \((AB)\) として並べていましたが、\((BA)\) と並べることもできるので、
\(120×2=240\) 通りです。

さて、 \(5\) つのものを横一列に並べましたが、左端と右端がくっついて、円形に並んでもらいましょう。
「回転しても同じ並びとみなす」ので、\(5\) つの重複ができます。
よって、\(240÷5=48\) 通りです。

（２）夫婦が向い合う

まず夫婦を座らせます。
\(2\) 人の円順列なので、\((2-1)!=1\) 通りです。

この \(1\) 通りは、公式うんぬんではなく、図をかいて確かめながら解いた方がわかりやすいですね。

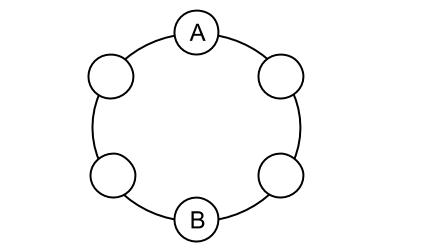
\(A\) がどこに座っても、\(B\) はその向かいに座るので枝分かれなし。
回転させても同じなので、上図の座り方のみ。
\(1\) 通りなのは当たり前じゃないですか！

次に、子ども \(4\) 人の座り方ですが、この \(4\) 人は、円順列とはなりません！

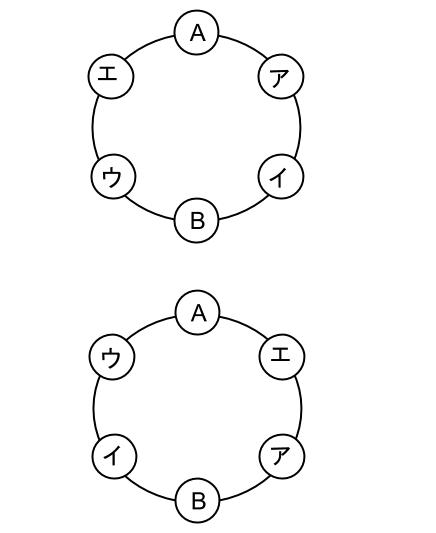
回転させても同じにならないことは図をみれば明らかでしょう。
アから見て時計回りにア、イ、ウ、エと子ども \(4\) 人が並ぶ座り方です。

まったく異なる座り方であり、重複していません。

よって、子ども \(4\) 人の座り方は、 \(4\) 人を並べる順列で、\(4!=24\) 通り

以上より、
\(1×24=24\) 通り

求まりました。

別解

まず、子ども \(4\) 人を座らせても解けます。
\(4\) 人の円順列なので、\((4-1)!=6\) 通りです。

次に、夫婦 \(2\) 人の座り方です。
\(A\) がどこに座るか考えると、下図の赤丸の箇所のどこかです。

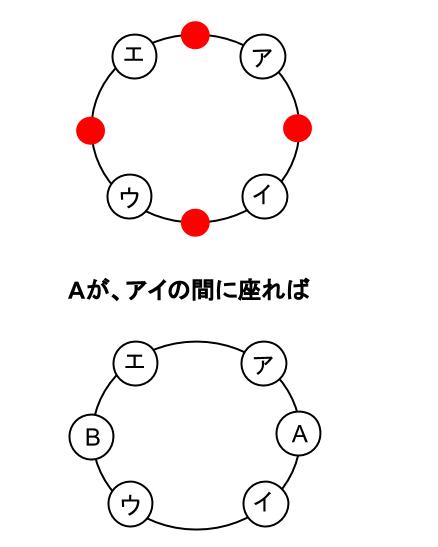
アとイの間
イとウの間
ウとエの間
エとアの間
の \(4\) 通りがあります。

\(A\) が座る位置が決まれば、\(B\) は自動的に決まるので、枝分かれはおきません。

よって、\(6×4=24\) 通りです。

数珠順列

数珠（じゅず）とは、お坊さんが持っているアレです。
真珠のようなものをつなげて、ネックレスや腕輪のようにしたものです。

例題１

赤、青、黄、緑の \(4\) つの球をひもに通し、輪にしてネックレスにします。
このようにして作られたネックレスの、異なる色の組み合わせは何通りですか。

解説

数珠＝ネックレス
同様のものだと考えてください。

数珠順列は、円順列の兄弟です。

じゅずは、裏返しがあるのです。

よって、数珠順列＝円順列\(÷2\)　と覚えましょう。

この問題では、
\((4-1)!÷2=3\) 通りです。

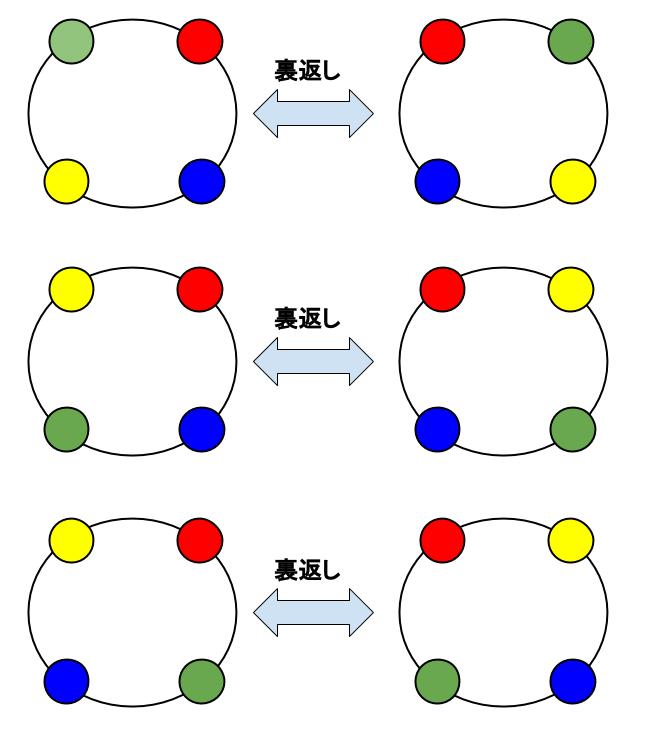
上図の \(6\) 通りは、円順列ならばすべて異なるものです。
\(4\) つの円順列の全 \(6\) 通りとなっています。

赤玉から時計まわりに回ってみてください。
青、黄色、緑の順列、\(6\) 通り、すべて異なっていることが確かめられます。

しかし、図に示した通りですが、左右で裏返しで同じになる組にできます。

数珠順列は、円順列の半分なのです。