センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

解説

まずは図示ですね。

薄くラフに下書きをして、概形を探ります。
\(\angle AOB=\angle BOC=\angle COA=60°\) ですから、対称的な図形であることがわかります。
正四面体を切断した形になります。

精密な図示は必ずしも必要ありませんが、図が正確なのは圧倒的有利になる可能性が高いです。日頃から作図の練習をして、図示を短時間で行えるようにしておきます。

正四面体の作図です。
コツは、底面の正三角形をまずかくこと。
頂点 \(O\) は、底面の重心の上にあるので、およその位置を決めて書きます。

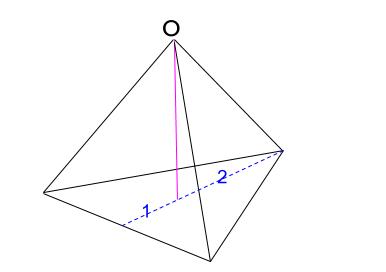
これはとても薄くかくのですよ。
ここに \(A,B,C\) を入れます。

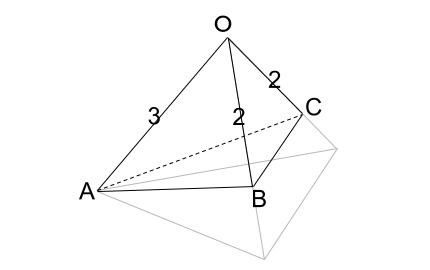
\(\overrightarrow{ a }\cdot \overrightarrow{ b }=\overrightarrow{ a }\cdot \overrightarrow{ c }=3\cdot2\cdot\cos 60°=3\) 、\(\overrightarrow{ b }\cdot \overrightarrow{ c }=2\cdot2\cdot\cos 60°=2\)

がすぐに計算できますね。
より、ア＝３、イ＝２

次は \(|\overrightarrow{ PQ }|^2=(ウs-エ)^2+(オt-カ)^2+キ\) です。

\(P,Q\) を図にいれましょう。

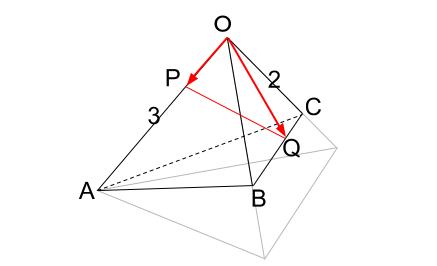
もちろん
\(\overrightarrow{ PQ }=\overrightarrow{ OQ }-\overrightarrow{ OP }\) です。

\(\overrightarrow{ OP }=s\overrightarrow{ a }\)
\(\overrightarrow{ OQ }=(1-t)\overrightarrow{ b }+t\overrightarrow{ c }\) と表すと直前にあるので、これを用いて計算するに決まっています。

\(\overrightarrow{ PQ }=\{(1-t)\overrightarrow{ b }+t\overrightarrow{ c }\}-s\overrightarrow{ a })\)

\(=-s\overrightarrow{ a }+(1-t)\overrightarrow{ b }+t\overrightarrow{ c }\)

もう覚悟を決めてがっつり計算しましょう。

\(|\overrightarrow{ PQ }|^2=\)\((-s\overrightarrow{ a }+(1-t)\overrightarrow{ b }+t\overrightarrow{ c })\cdot(-s\overrightarrow{ a }+(1-t)\overrightarrow{ b }+t\overrightarrow{ c })\)

\(=s^2|\overrightarrow{ a }|^2+(1-t)^2|\overrightarrow{ b }|^2+t^2|\overrightarrow{ c }|^2\)
\(-2s(1-t)\overrightarrow{ a }\cdot\overrightarrow{ b }-2st\overrightarrow{ a }\cdot\overrightarrow{ c }\)\(+2t(1-t)\overrightarrow{ b }\cdot\overrightarrow{ c }\)

\(=9s^2+4(1-t)^2+4t^2-3\cdot2s(1-t)\)\(-3\cdot2st+2\cdot2t(1-t)\)

\(=9s^2-6s+4t^2-4t+4\)

目標の穴の形に合わせるには、\(s,t\) をそれぞれ平方完成ですね。

\(9s^2-6s+4t^2-4t+4\)

\(=(3s-1)^2-1+(2t-1)^2-1+4\)

\(=(3s-1)^2+(2t-1)^2+2\)

より、ウ＝３、エ＝１、オ＝２、カ＝１、キ＝２

\(|\overrightarrow{ PQ }|^2=(3s-1)^2+(2t-1)^2+2\)
であることが求まって、次に\(\overrightarrow{ PQ }\) の最小値です。

\(\overrightarrow{ PQ }\) はもちろん正です。

よって、\(\overrightarrow{ PQ }\) が最小のとき、\(|\overrightarrow{ PQ }|^2\) が最小です。

\(|\overrightarrow{ PQ }|^2\) の最小値は、

\(0 \leqq (3s-1)^2\) かつ \(0 \leqq (2t-1)^2\) なので、

\( (3s-1)^2=0\) かつ \((2t-1)^2=0 \) のとき

つまり、\(s=\displaystyle \frac{1}{3}\) 、 \(t=\displaystyle \frac{1}{2}\) のときであり、

このとき、\(|\overrightarrow{ PQ }|^2=0+0+2=2\)

より、\(|\overrightarrow{ PQ }|=\sqrt{2}\)

ク＝１、ケ＝３、コ＝１、サ＝２、シ＝２

さて後半戦へ！

解説

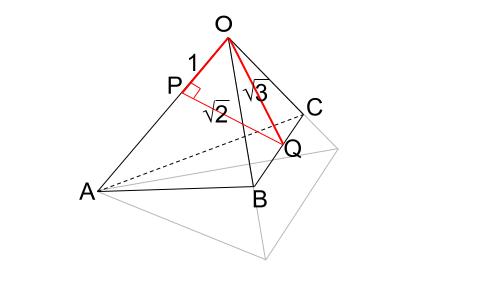
\(|\overrightarrow{ PQ }|=\sqrt{シ}\) のときを考えるので、先ほど求まった値を図に入れていきます。

\(|\overrightarrow{ PQ }|=\sqrt{2}\)

また、\(s=\displaystyle \frac{1}{3}\) 、 \(t=\displaystyle \frac{1}{2}\) のときなので、

\(\overrightarrow{ OP }=s\overrightarrow{ a }=\displaystyle \frac{1}{3}\overrightarrow{ a }\)

\(\overrightarrow{ OQ }=(1-t)\overrightarrow{ b }+t\overrightarrow{ c }=\displaystyle \frac{1}{2} \overrightarrow{ b }+\displaystyle \frac{1}{2} \overrightarrow{ c }\)

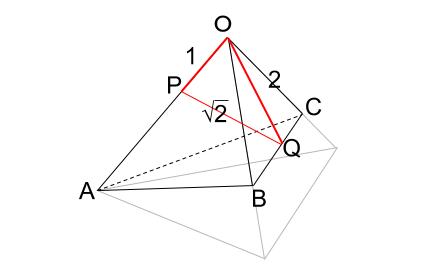
※\(Q\) は \(BC\) の中点

さて、 \(\overrightarrow{ OA }\cdot \overrightarrow{ PQ }=ス\) から、\(\angle APQ=セソ°\) である。とあります。

内積の値から、\(\cos \angle APQ\) が求まり、\(\angle APQ\) が求まるという大定番の流れであることは一目瞭然です。

正攻法ならば、がっつりベクトルの計算をするわけですが、だいたい図を見れば検討がつきますね。

そもそも、\(\angle APQ=セソ°\) に入る角は、\(30,45,60,90\) しかありえません。

\(\cos \angle APQ\) から求まるのですから、有名角です。

図は正確にかかれたものではありませんけど、\(\angle APQ=90°\) と予想されます。

実際に成り立つのかは、三角形 \(OPQ\) に三平方の定理を用いて確かめられます。

\(OQ\) は 辺の長さが \(2\) の正三角形の高さなので、\(\sqrt{3}\)

\(\angle APQ=90°\) ならば、
\(1^2+(\sqrt{2})^2=(\sqrt{3})^2\)

成り立っています！

よって、
\(\overrightarrow{ OA }\cdot \overrightarrow{ PQ }=0\) から、\(\angle APQ=90°\)

ス＝０、セ＝９、ソ＝０

この結果から、三角形 \(APQ\) の面積は \(\sqrt{タ}\) は、

\(2×\sqrt{2}×\displaystyle \frac{1}{2}=\sqrt{2}\)

より、タ＝２

正攻法のベクトルの計算

上のように楽をしなければ、ベクトルの計算をがっつりすることになります。

\(\overrightarrow{ PQ }=-\displaystyle \frac{1}{3}\overrightarrow{ a }+\displaystyle \frac{1}{2}\overrightarrow{ b }+\displaystyle \frac{1}{2}\overrightarrow{ c }\)

\(\overrightarrow{ OA }=\overrightarrow{ a }\)

より、

\(\overrightarrow{ OA }\cdot \overrightarrow{ PQ }=\overrightarrow{ a }\cdot(-\displaystyle \frac{1}{3}\overrightarrow{ a }+\displaystyle \frac{1}{2}\overrightarrow{ b }+\displaystyle \frac{1}{2}\overrightarrow{ c })\)

\(=-\displaystyle \frac{1}{3}|\overrightarrow{ a }|^2+\displaystyle \frac{1}{2}\overrightarrow{ a }\cdot\overrightarrow{ b }+\displaystyle \frac{1}{2}\overrightarrow{ a }\cdot\overrightarrow{ c }\)

\(=-\displaystyle \frac{9}{3}+\displaystyle \frac{3}{2}+\displaystyle \frac{3}{2}=0\)

では続きです。

また、

\(\overrightarrow{ OG }=\displaystyle \frac{チ}{ツ}\overrightarrow{ OA }+ \displaystyle \frac{テ}{ト}\overrightarrow{ OQ }\)

であり、点 \(G\) は線分 \(AQ\) を \(ナ:1\) に内分する点である。

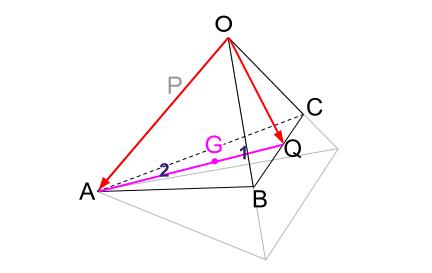
三角形 \(ABC\) の重心を \(G\) とするとありますので、図示しましょう。
点 \(Q\) は \(BC\) の中点です。そして、\(AQ\) を \(2:1\) に内分する位置が \(G\) です。

よって、

\(\overrightarrow{ OG }=\displaystyle \frac{1}{3}\overrightarrow{ OA }+ \displaystyle \frac{2}{3}\overrightarrow{ OQ }\)

より、チ＝１、ツ＝３、テ＝２、ト＝３、ナ＝２

以上のことから、三角形 \(GPQ\) の面積は三角形 \(APQ\) の面積の \(\displaystyle \frac{1}{3}\) なので、

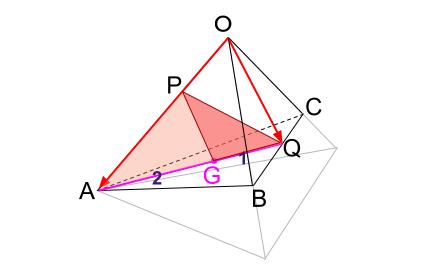
\(\sqrt{2}×\displaystyle \frac{1}{3}=\displaystyle \frac{\sqrt{2}}{3}\)

より、二＝２、ヌ＝３