【センター試験ⅡＢ】平面ベクトル０２

センター試験・過去問研究

センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう！

$a$ を $0 \lt a \lt 1$ を満たす定数とする。三角形 $ABC$ を考え、辺 $AB$ を $1:3$ に内分する点を $D$、辺 $BC$ を $a:(1-a)$ に内分する点を $E$、直線 $AE$ と直線 $CD$ の交点を $F$ とする。$\overrightarrow{ FA } = \overrightarrow{ p }$、$\overrightarrow{ FB } =\overrightarrow{ q }$、$\overrightarrow{ FC } = \overrightarrow{ r}$ とおく。

（１）$\overrightarrow{ AB }=ア$ であり

$|\overrightarrow{ AB }|^2=|\overrightarrow{ p }|^2-イ\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$・・・①

である。ただし、$ア$ については、当てはまるものを、次の０～３のうちから一つ選べ。

０ $\overrightarrow{ p }+\overrightarrow{ q }$
１ $\overrightarrow{ p }-\overrightarrow{ q }$
２ $\overrightarrow{ q }-\overrightarrow{ p }$
３ $-\overrightarrow{ p }-\overrightarrow{ q }$

筆者注　続く

まずはざっと図示をしましょう。

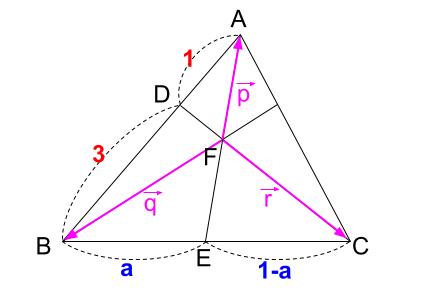
$高校数学無料学習サイトko-su- センター試験　平面ベクトル1001$

なにやら、チェバの定理を使えそうな図ですね。
実際、図形的に解いていくことも可能です。

まずは、ベクトルらしく、計算処理で解いていく解法からです。
最後に、図形的な処理についても解説します。

$\overrightarrow{ AB }=\overrightarrow{ FB }-\overrightarrow{ FA }$

$=\overrightarrow{ q }-\overrightarrow{ p }$

より、$ア$ は選択肢２です。

ア＝２

（２）$\overrightarrow{ FD }$ を $\overrightarrow{ p }$ と $\overrightarrow{ q }$ を用いて表すと

$\overrightarrow{ FD }=\displaystyle \frac{ウ}{エ}\overrightarrow{ p }+\displaystyle \frac{オ}{カ}\overrightarrow{ q }$・・・②

である。

内分の基礎公式通りですね。

$\overrightarrow{ FD }=\displaystyle \frac{3}{1+3}\overrightarrow{ p }+\displaystyle \frac{1}{1+3}\overrightarrow{ q }$

$=\displaystyle \frac{3}{4}\overrightarrow{ p }+\displaystyle \frac{1}{4}\overrightarrow{ q }$

より、ウ＝３、エ＝４、オ＝１、カ＝４

ここまで、基礎の基礎の基礎ってところですね。

（３）$s,t$ をそれぞれ $\overrightarrow{ FD }=s \overrightarrow{ r },\overrightarrow{ FE }=t \overrightarrow{ p }$ となる実数とする。$s$ と $t$ を $a$ を用いて表そう。

$\overrightarrow{ FD }=s \overrightarrow{ r }$ であるから、②により

$\overrightarrow{ q }=キク \overrightarrow{ p }+ケs \overrightarrow{ r }$・・・③

である。また、 $\overrightarrow{ FE }=t \overrightarrow{ p }$ であるから

$\overrightarrow{ q }=\displaystyle \frac{t}{コ-サ} \overrightarrow{ p }-\displaystyle \frac{シ}{コ-サ} \overrightarrow{ r }$・・・④

である。③と④により

$s=\displaystyle \frac{スセ}{ソ(コ-サ)}$ 、$t=タチ(コ-サ)$

である。

$\overrightarrow{ FD }=s \overrightarrow{ r }$ であるから、②により $\overrightarrow{ q }=キク \overrightarrow{ p }+ケs \overrightarrow{ r }$ とありますね。

②は、$\overrightarrow{ FD }=\displaystyle \frac{3}{4}\overrightarrow{ p }+\displaystyle \frac{1}{4}\overrightarrow{ q }$

なので、$s \overrightarrow{ r }=\displaystyle \frac{3}{4}\overrightarrow{ p }+\displaystyle \frac{1}{4}\overrightarrow{ q }$

これを式変形すれば、
$\overrightarrow{ q }=-3 \overrightarrow{ p }+4s \overrightarrow{ r }$・・・③

より、キク＝ー３、ケ＝４

次に、 $\overrightarrow{ FE }=t \overrightarrow{ p }$ であるから、$\overrightarrow{ q }=\displaystyle \frac{t}{コ-サ} \overrightarrow{ p }-\displaystyle \frac{シ}{コ-サ} \overrightarrow{ r }$ をうめます。

先ほどと同じステップを踏めば、まずは、

$\overrightarrow{ FE }=(1-a)\overrightarrow{ q }+a\overrightarrow{ r }$

$\overrightarrow{ FE }=t \overrightarrow{ p }$ であるから

$ t\overrightarrow{ p }=(1-a)\overrightarrow{ q }+a\overrightarrow{ r }$

これを式変形すれば、

$\overrightarrow{ q }=\displaystyle \frac{t}{1-a} \overrightarrow{ p }-\displaystyle \frac{a}{1-a} \overrightarrow{ r }$・・・④

より、コ＝１、サ＝a、シ＝a

③と④により $s=\displaystyle \frac{スセ}{ソ(コ-サ)}$ 、$t=タチ(コ-サ)$ を埋めます。

③、④はどちらも $\overrightarrow{ q }$ を、$\overrightarrow{ p },\overrightarrow{ r }$ で表した式ですから、係数比較をせよ、ということですね。

$\overrightarrow{ q }=-3 \overrightarrow{ p }+4s \overrightarrow{ r }$・・・③

$\overrightarrow{ q }=\displaystyle \frac{t}{1-a} \overrightarrow{ p }-\displaystyle \frac{a}{1-a} \overrightarrow{ r }$・・・④

ですね。
$\overrightarrow{ p }$ の係数より、

$-3=\displaystyle \frac{t}{1-a}$

より、$t=-3(1-a)$

より、タチ＝-3

$\overrightarrow{ r }$ の係数より、

$4s=-\displaystyle \frac{a}{1-a}$

より、$s=\displaystyle \frac{-a}{4(1-a)}$

より、スセ＝－a、ソ＝４

（４）$|\overrightarrow{ AB }|=|\overrightarrow{ BE }|$ とする。$|\overrightarrow{ p }|=1$ のとき、$\overrightarrow{ p }$ と $\overrightarrow{ q }$ の内積を $a$ を
用いて表そう。

①により

$|\overrightarrow{ AB }|^2=1-イ\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$

である。また

$|\overrightarrow{ BE }|^2=$$ツ(コ-サ)^2+テ(コ-サ)\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$

である。したがって

$\overrightarrow{ p } \cdot \overrightarrow{ q }=\displaystyle \frac{トナ-ニ}{ヌ}$

である。

$イ=2$ ははじめに求めています。

$\overrightarrow{ BE }=\overrightarrow{ FE }-\overrightarrow{ FB }$

$=t\overrightarrow{ p } -\overrightarrow{ q } $

$=-3(1-a)\overrightarrow{ p } -\overrightarrow{ q } $

$|\overrightarrow{ BE }|^2$$=9(1-a)^2|\overrightarrow{ p }|^2+6(1-a)\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$

$|\overrightarrow{ p }|=1$ なので、

$|\overrightarrow{ BE }|^2$$=9(1-a)^2+6(1-a)\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$

より、ツ＝９、テ＝６

いよいよ最後です。

$|\overrightarrow{ AB }|=|\overrightarrow{ BE }|$ としているので、

$|\overrightarrow{ AB }|^2=|\overrightarrow{ BE }|^2$ なので、

$1-2\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$$=9(1-a)^2+6(1-a)\overrightarrow{ p } \cdot \overrightarrow{ q }+|\overrightarrow{ q }|^2$

どんどん式変形していきます。

$1-2\overrightarrow{ p } \cdot \overrightarrow{ q }$$=9(1-a)^2+6(1-a)\overrightarrow{ p } \cdot \overrightarrow{ q }$

$1-9(1-a)^2=6(1-a)\overrightarrow{ p } \cdot \overrightarrow{ q }+2\overrightarrow{ p } \cdot \overrightarrow{ q }$

$1-(9-18a+9a^2)=2(4-3a)\overrightarrow{ p } \cdot \overrightarrow{ q }$

$-8+18a-9a^2=2(4-3a)\overrightarrow{ p } \cdot \overrightarrow{ q }$

$-(3a-4)(3a-2)=2(4-3a)\overrightarrow{ p } \cdot \overrightarrow{ q }$

$\overrightarrow{ p } \cdot \overrightarrow{ q }=\displaystyle \frac{3a-2}{2}$

より、トナ＝３a、二＝２、ヌ＝２

以上です。

別解として、図形的処理についても書きます。
ぜひ学習して、ベクトルの問題を多面的に解けるようになりましょう。

参考・チェバの定理

問題の誘導にのっとって、ベクトルの計算をして解答してきました。
本問はとても簡単で、計算も面倒ではありませんから、この方針で何の問題もありません。
さて、本問の図は・・チェバの定理が頭に浮かびますね・・・

チェバの定理をはじめ、図形的に解くことも可能です。

見ていきましょう。

$BF$ の延長線と $AC$ の交点を、$G$ とおきます。

$高校数学無料学習サイトko-su- センター試験　平面ベクトル1003$

まずはチェバの定理を適用します。

点 $A$ から反時計まわりにまわると、

$\displaystyle \frac{1}{3}×\displaystyle \frac{a}{1-a}×\displaystyle \frac{CG}{GA}=1$

より、$\displaystyle \frac{CG}{GA}=\displaystyle \frac{3(1-a)}{a}$

$高校数学無料学習サイトko-su- センター試験　平面ベクトル1004$

そして、それぞれの辺の比から、以下の $3$ つの三角形の面積比がわかります。

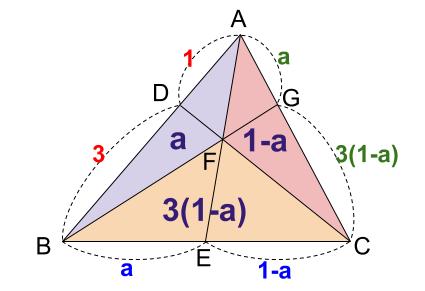
$高校数学無料学習サイトko-su- センター試験　平面ベクトル1011$

より、下図の面積比は、$a:4(1-a)$

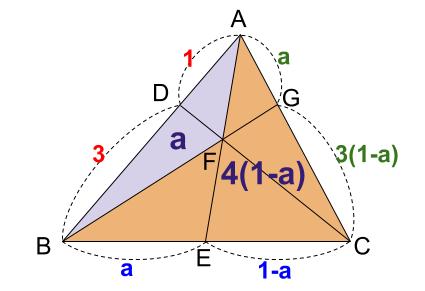
$高校数学無料学習サイトko-su- センター試験　平面ベクトル10122$

これは、$DF:FC$ の長さの比と一致します。

よって、$\overrightarrow{ FD }=-\displaystyle \frac{a}{4(1-a)}\overrightarrow{ FC }$

$\overrightarrow{ FC }=\overrightarrow{ r }$
$\overrightarrow{ FD }=s \overrightarrow{ r }$

とおいているので、

$s=-\displaystyle \frac{a}{4(1-a)}$

これにより（３）の、コ、サ、ス、セ、ソが求まりました。

また、下図の面積比は、$1:3(1-a)$

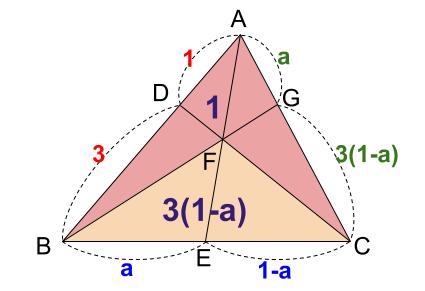
$高校数学無料学習サイトko-su- センター試験　平面ベクトル1013$

これは、$AF:FE$ の長さの比と一致します。

よって、$\overrightarrow{ FE }=-3(1-a)\overrightarrow{ FA }$

$\overrightarrow{ FA }=\overrightarrow{ p }$
$\overrightarrow{ FE }=t \overrightarrow{ p }$

とおいているので、

$t=-3(1-a)$

これにより（３）の、タ、チが求まりました。

さらに、面積比とベクトルには以下の性質があります。

$高校数学無料学習サイトko-su- センター試験　平面ベクトル1014$

↑上図のとき

$3(1-a)\overrightarrow{ p }+(1-a)\overrightarrow{ q }+a\overrightarrow{ r }=0$・・・（Ⅰ）

それぞれのベクトルの後ろにある三角形の面積を係数として、和を取ると $0$ になります。

非常に美しく、覚えやすい性質です。役に立つ機会も多いので、ぜひ覚えておきましょう。

本問では、先ほど求めた $s,t$ と合わせて、

④式の穴を埋めることができます。

$\overrightarrow{ q }=\displaystyle \frac{t}{コ-サ} \overrightarrow{ p }-\displaystyle \frac{シ}{コ-サ}\overrightarrow{ r }$・・・④

$s=-\displaystyle \frac{a}{4(1-a)}$

$t=-3(1-a)$

コ＝１、サ＝４も求まっているので、

④式は、

$\overrightarrow{ q }=\displaystyle \frac{t}{1-a} \overrightarrow{ p }-\displaystyle \frac{シ}{1-a}\overrightarrow{ r }$

$3(1-a)\overrightarrow{ p }+(1-a)\overrightarrow{ q }+a\overrightarrow{ r }=0$・・・（Ⅰ）
を変形すると

$\overrightarrow{ q }=-3 \overrightarrow{ p }-\displaystyle \frac{a}{1-a} \overrightarrow{ r }$

係数を比較することにより、シ＝a

$t=-3(1-a)$ なので、一致しています。

カテゴリー: センター試験ⅡB、作成途中