定数項に文字を含む３次方程式

定数項に文字を含む \(3\) 次方程式は、文字を分離して考えます。

\(y=f(x)\) と \(y=P\) の共有点の \(x\)座標が、方程式の解だからです。

例題１

\(x\) の \(3\) 次方程式 \(x^3-12x+2=a\) が異なる実数解を \(3\) 個もつとき、定数 \(a\) の値の範囲を求めなさい。

解説

\(x\) の \(3\) 次方程式 \(x^3-12x+2=a\) の解の個数は、
\(y=x^3-12x+2\) のグラフと \(y=a\) の共有点の個数に等しい。

\(f(x)=x^3-12x+2\) とすると

\(f´(x)=3x^2-12\)
\(=3(x+2)(x-2)\)

\(f´(x)=0\) のとき \(x= \pm 2\)

\(\begin{array}{c|ccccc}
x & \cdots & -2 & \cdots & 2 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 18 & \searrow & -14 & \nearrow\end{array}\)

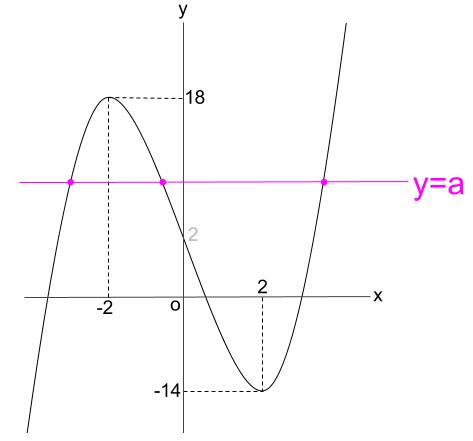
よって、グラフより異なる実数解を \(3\) つもつような定数 \(a\) の値の範囲は
\(-14 \lt a \lt 18\)

さらに詳しく

グラフより異なる実数解を \(1\)つもつとき、 \(2\)つもつときの定数 \(a\) の値の範囲もわかります。

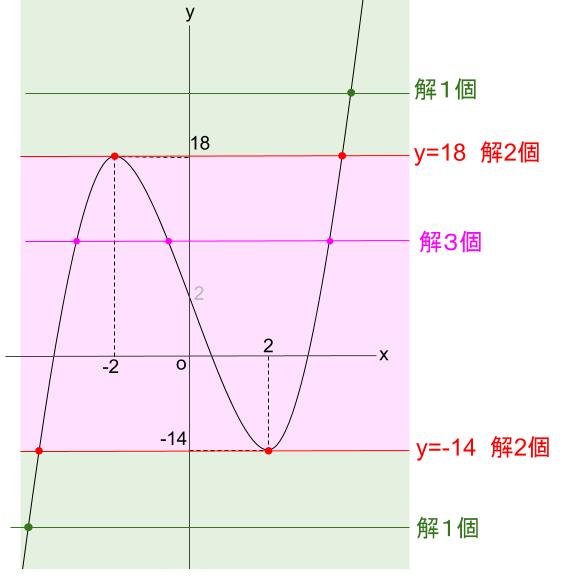
グラフより、
\(a \lt -14, 18 \lt a\) のとき、実数解を \(1\)つもつ
\(a=-14,18\) のとき、実数解を \(2\)つもつ
\(-14 \lt a \lt 18\) のとき、実数解を \(3\)つもつ

例題２

\(x\) の \(3\) 次方程式 \(x^3-3x^2-9x-a+10=0\) が異なる \(2\) 個の正の解と \(1\) 個の負の解をもつとき、
定数 \(a\) の値の範囲を求めなさい。

解説

\(x^3-3x^2-9x-a+10=0\)
の \(a\) を右辺に移項すると
\(x^3-3x^2-9x+10=a\)

つまり、
\(y=x^3-3x^2-9x+10\) のグラフと \(y=a\) の共有点の \(x\) 座標が、
正で \(2\) 個、負で \(1\) 個となる定数 \(a\) の値の範囲を求めたいのです。

\(f(x)=x^3-3x^2-9x+10\) とすると

\(f´(x)=3x^2-6x-9\)
\(=3(x+1)(x-3)\)

\(f´(x)=0\) のとき \(x=-1,3\)

\(\begin{array}{c|ccccc}
x & \cdots & -1 & \cdots & 3 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 15 & \searrow & -17 & \nearrow\end{array}\)

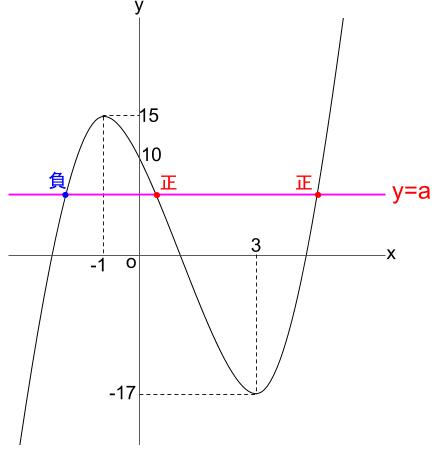
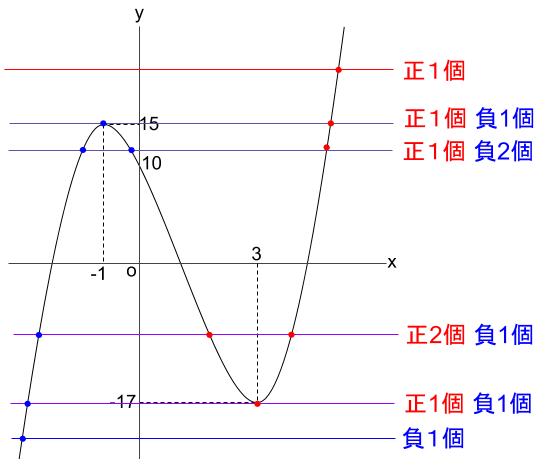
よって、グラフより \(-17 \lt a \lt 10\)

ちなみに、他の範囲は下図のようになります。