2次関数の決定 最大値・最小値
\(2\) 次関数の決定 最大値・最小値
最大値・最小値の情報から、\(2\) 次関数を決定します。
頂点や、定義域の端で最大値・最小値をとりますから、
そこから決定していきます。
例題1
\(x=1\) で最大値 \(-2\) をとり、\(x=3\) で \(y=-6\) となるような \(2\) 次関数を求めなさい。
解説
まずグラフが上に凸か、下に凸か、どちらかが決定できます。
\(x=1\) で最大値 \(-2\) をとるということは、
下図のようになっています。上に凸ですね。

※ \(x,y\) 軸は、本問では必要ありません。
つまり、このグラフの頂点が \((1,-2)\) と与えられたということです。
よって求める \(2\) 次関数の式は、
\(y=a(x-1)^2-2\) とおけます。
あとは、通る点をこの式に代入すれば、\(a\) が求まりますね。
\(y=a(x-1)^2-2\) に \(x=3\) と \(y=-6\) を代入して
\(-6=a(3-1)^2-2\)
これを解いて、\(a=-1\)
よって求める \(2\) 次関数の式は、
\(y=-(x-1)^2-2\)
\(y=-x^2+2x-3\)
例題2
関数 \(y=2x^2-4x+c\)、\((-1 \leqq x \leqq 2)\)
の最大値が \(5\) であるとき、定数 \(c\) の値を求めなさい。
また、最小値を求めなさい。
解説
最大値、最小値はグラフの概形を考えます。
可能な限り、数学は目で見て解きます。
図示ができる問題は図示して、目て見て解きたいという欲求を持ってください。
ですから、平方完成です。
\(y=2x^2-4x+c\)
\(y=2(x-1)^2-2+c\)
頂点が \((1,-2+c)\) であることがわかります。
\(x\) 軸がどこにあるのかわかりませんので、
わからないなりの図示をします。
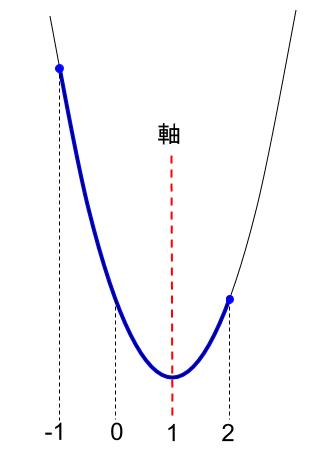
定義域 \(-1 \leqq x \leqq 2\) は、青い太い部分です。
\(2\) 次関数は軸を中心に左右対称なのは知っていますか?
知らなかったら必ず今暗記してください!!
よって、軸の \(x=1\) から最も離れた点で、最大値を取ります。
上のグラフより、
最大値は \(x=-1\) を関数 \(y=2x^2-4x+c\) 代入して、
\(2(-1)^2-4(-1)+c\)
\(=6+c\)
最大値は \(5\) なので
\(5=6+c\)
より \(c=-1\)
最小値は、\(x=1\) の頂点でとります。
頂点が \((1,-2+c)\) なので、
最小値は \(-2+c\) です。
\(c=-1\) なので、
\(-2+c=-3\)
よって、最小値は \(-3\) です。