2次関数の平方完成
平方完成
\(2\) 次関数の学習の一番はじめに
\(y=2x^2\) を
\(x\) 軸方向に \(+3\)
\(y\) 軸方向に \(-1\)
平行移動させると、
\(y-(-1)=2(x-3)^2\)
この式を変形していくと・・・
\(y+1=2(x^2-6x+9)\)
\(y+1=2x^2-12x+18\)
\(y=2x^2-12x+17\)
ということを見ました。
もちろんですが、
この計算の逆の操作が重要になります。
はじめに
\(y=2x^2-12x+17\)
と式が与えられたとき、
これを式変形することによって
\(y-1=2(x-3)^2\)
という形にするのです。
この形にすることで、頂点が \((3,1)\) とわかるため、
\(y=2x^2-12x+17\)
のグラフの概形を図示できます。
この式変形を「平方完成」といいます。
\(y=ax^2+bx+c\) を
\(y=a(x-p)^2+q\)
に式変形することです。
※ \(2\) 次方程式を解くときにも「平方完成」がありましたね。
そっくりな計算技術です!
※\(y-q=a(x-p)^2\) でも、もちろん同じことです。
具体例1
\(y=x^2+6x+1\) のグラフをかきなさい。
解説
平方完成という式変形をすることで、
放物線の頂点を求めることができます。
あとは \(y=x^2\) と同じような曲線をかきます。
では平方完成です。
\(y=x^2+6x+1\)・・・ア
を式変形して、
\(y=a(x-p)^2+q\)・・・イ
の形にするのが目的です。
イを展開したら、アに等しくなる、
そのためには、
\(a=1\) がわかりますね。
イに代入します。
\(y=x^2+6x+1\)・・・ア
\(y=(x-p)^2+q\)・・・イ
さらに、イを展開して、アと等しくなるためには、
\(x\) の \(1\) 次の項の係数に着目して、
\(p=-3\) です。
イに代入します。
\(y=x^2+6x+1\)・・・ア
\(y=(x+3)^2+q\)・・・イ
イの式を展開してみれば、
\(y=(x+3)^2+q\)
\(=x^2+6x+9+q\)
これがアの式、\(y=x^2+6x+1\) と等しくなるためには、
\(q=-8\) です。
よって、\(y=x^2+6x+1\) は平方完成によって、
\(y=(x+3)^2-8\)
となります。
これは、\(y=x^2\) のグラフを
\(x\) 軸方向に \(-3\)
\(y\) 軸方向に \(-8\)
平行移動したものなので頂点が \((-3,-8)\) で、下に凸の放物線になります。
グラフをかくとき、比率などの正確性はあまり気にしなくてよいですが、
\(y\) 軸や \(x\) 軸との交点には意識しましょう。
交点の符号が正か負かは意識します。
\(x=0\) のとき、\(y=1\) なので、下図のようになります。
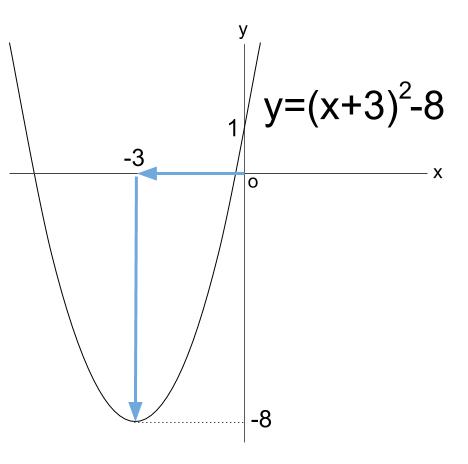
※上図の矢印は解答にはいらないです。
頂点の平行移動を表しています。
平方完成の手順を公式化する
上の例の解説のように、係数を比較しながら平方完成をすることもできますが、
機械的に公式化するならば、
\(x\) の \(1\) 次の項の係数の半分を求め、それを \(2\) 乗します。
その値を与式に足して、引くことで、平方完成ができます。
?何言ってるの?って感じの文章ですね(笑)。
具体例で見ていきましょう。
\(y=x^2+6x+1\) を平方完成しましょう。
\(x\) の \(1\) 次の項の係数の半分 \(3\) を、 \(2\) 乗して \(9\) です。
その \(9\) を、足して、引きます。
\(y=x^2+6x\)\(+9\)\(-9\)\(+1\)
※\(x^2,x\) の項の次にこの操作を入れます。
右辺の前半を平方の公式で因数分解します。
\(y=\)\(\underline{(x^2+6x+9)}\) \(-9+1\)
\(y=\)\(\underline{(x+3)^2}\) \(-9+1\)
定数項をまとめます。
\(y=(x+3)^2-8\)
平方完成、完了です!!
具体例2
\(y=-2x^2+8x+1\) のグラフをかきなさい。
解説
これを平方完成するのは、はじめての人にはかなり難しいです。
やり方は、自力で導出する必要はありません。
下の手順を見て、やり方をマスターしましょう。
手順1 \(x^2\) の項と \(x\) の項を、\(x^2\) の項の係数でくくる
\(y=-2x^2+8x+1\)
の \(x^2\) の項と \(x\) の項を、\(-2\) でくくります。
\(y=-2(x^2-4x)+1\)
とにかく手順として覚えればOKですが、なぜこうするかというと、
目指す最終目標は、
\(y=a(x-p)^2+q\) だからです。
平方の公式で因数分解するとき、
\(x^2\) の項の係数を \(1\) にして行うからです。
手順2 くくった( )かっこの中で平方完成をする
\(y=-2(x^2-4x)+1\)
の
\((x^2-4x)\)
の部分だけを変形します。
もちろん平方完成です。
\(x\) の \(1\) 次の項の係数の半分である \(-2\) を \(2\) 乗して \(4\) です。
その値を足して、引いて、平方完成します。
\(y=-2(x^2-4x)+1\)
\(y=-2(x^2-4x\)\(+4\)\(-4\)\()+1\)
\(y=-2\{(\underline{x^2-4x+4})-4\}+1\)
\(y=-2\{\underline{(x-2)^2}-4\}+1\)
ここまでくれば、あとは調整です。
\((x-2)^2\) 以外の部分を展開して、定数項をまとめます。
\(y=-2(x-2)^2+8+1\)
\(y=-2(x-2)^2+9\)
これで平方完成が完了しました。
よって、頂点が \(2,9\) で上に凸な放物線です。
\(x=0\) のとき、\(y=1\) なので、下図のようになります。
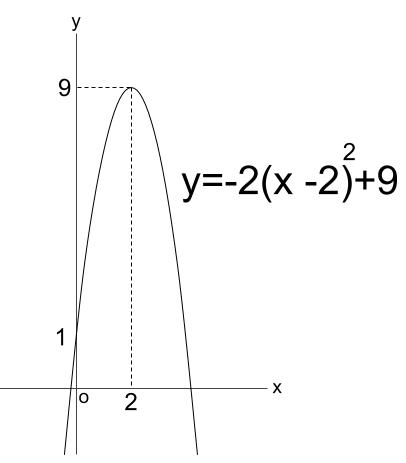
別解
平方完成の途中経過は、
自分がわかりやすい、やりやすい、と感じるものでOKです。
計算のつじつまさえあっていれば、過程はなんでもよいのです。
はじめに見た、係数比較をすることで平方完成をしてみましょう。
\(y=-2x^2+8x+1\)
を平方完成をして、
\(y=-2(x-p)^2+q\) の形にしたい。
※この形が最終目標であることは大丈夫でしょうか?
\(y=-2x^2+8x+1\) ・・・ア
\(y=-2(x-p)^2+q\) ・・・イ
イを展開するとアになります。
\(x\) の \(1\) 次の項の係数から、
\(p=2\) なので、イに代入します。
\(y=-2(x-2)^2+q\) ・・・イ
これを展開すると、
\(y=-2(x^2-4x+4)+q\)
\(y=-2x^2+8x-8+q\)
これがアの式、\(y=-2x^2+8x+1\) と等しくなるので、
\(q\) は \(+9\)
よって、
\(y=-2(x-2)^2+9\)
これで平方完成は完了です。
参考・すべての \(2\) 次関数\(y=ax^2+bx+c\) は \(y=ax^2\) の平行移動である
ちなみに、すべての \(2\) 次式で、この式変形が可能ですね。
つまり、
\(y=ax^2+bx+c\) は必ず、
\(y=a(x-p)^2+q\)
の形に変形することができます。
よって、\(y=ax^2+bx+c\) は、\(y=ax^2\) を平行移動したものと言えるわけです。