【センター試験ⅠA】2次不等式02
センター試験・過去問研究
センター試験の過去問を徹底解説します。
センター試験とはどれくらいのレベルの問題が出るのか、どのような出題があるのか、まずは経験値をつみましょう!
\(a\) を正の実数とし
\(f(x)=ax^2-2(a+3)x-3a+21\)
とする。 \(2\) 次関数 \(y=f(x)\) のグラフの頂点の \(x\) 座標を \(p\) とおくと
\(p=サ+\displaystyle \frac{シ}{a} \)
である。
筆者注 続く
解説
\(2\) 次関数のグラフの頂点ですから、平方完成に決まっていますね。
\(f(x)=ax^2-2(a+3)x-3a+21\)
\(=a\{x^2-\displaystyle \frac{2(a+3)}{a}x\}-3a+21\)
\(=a\{x-\displaystyle \frac{(a+3)}{a}\}^2-\displaystyle \frac{(a+3)^2}{a}-3a+21\)
より、グラフの頂点の \(x\) 座標は \(\displaystyle \frac{a+3}{a}=1+\displaystyle \frac{3}{a}\)
より、サ=1、シ=3
\(a\) は正の実数なので、下のような図になります。
\(x\) 軸の位置は不明です。
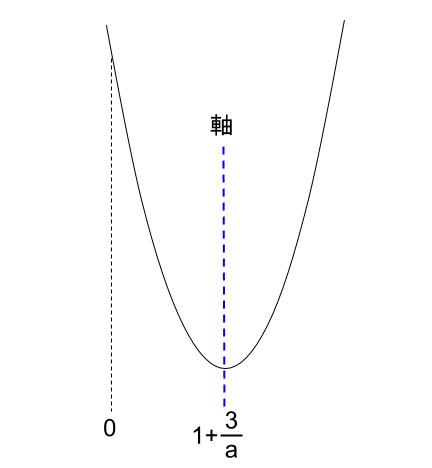
\(0 \lt a \leqq ス\)
である。
筆者注 続く
もちろん図示して考えます。\(0 \leqq x \leqq 4\) での最小値が \(f(4)\) なので、
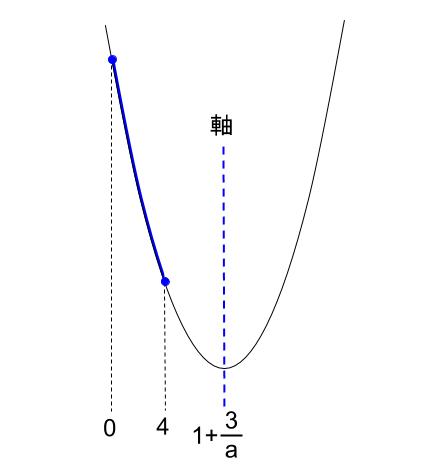
あるいは
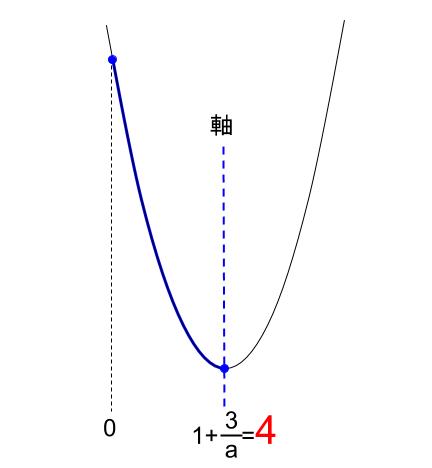
のときです。
つまり2つ合わせて、\(4 \leqq 1+\displaystyle \frac{3}{a}\)
式を整理すると
\(a \leqq 1\)
\(a\) は正の実数なので、
\(0 \lt a \leqq 1\)
よりス=1
\(セ \leqq a\)
である。
筆者注 続く
もちろん図示します。
\(p\) はグラフの頂点の \(x\) 座標なので(問題のはじめの方にあり)
頂点で最小値です。

あるいは
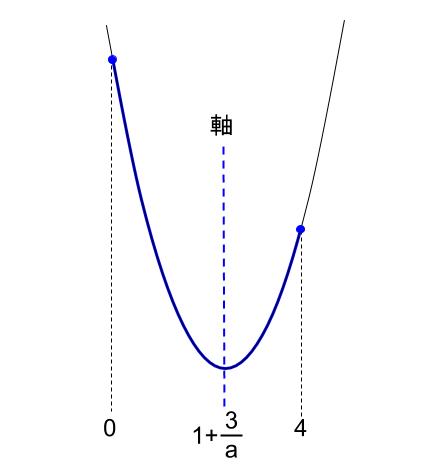
のときです。
つまり2つ合わせて、\(1+\displaystyle \frac{3}{a} \leqq 4\)
※\(a\) は正の実数なので、\(0 \leqq 1+\displaystyle \frac{3}{a} \) は自動的に満たします。
よって、
\(1+\displaystyle \frac{3}{a} \leqq 4\)
を満たす範囲を求めます。
\(\displaystyle \frac{3}{a} \leqq 3\)
\(\displaystyle \frac{1}{a} \leqq 1\)
\(1 \leqq a\)
より、セ=1
\(a=\displaystyle \frac{ソ}{タ} \)
\(a=\displaystyle \frac{チ+\sqrt{ツテ}}{ト} \)
のときである。
筆者注 以上
今まで見てきた \(2\) 通りの場合分け、それぞれで求めます。
\(y=f(x)\) の最小値が \(f(4)\) のとき
\(f(x)=ax^2-2(a+3)x-3a+21\) なので、
\(f(4)=a\cdot 4^2-2(a+3)\cdot 4-3a+21\)
\(=16a-8(a+3)-3a+21\)
\(=5a-3\)
これが最小値 \(1\) になるので、
\(5a-3=1\)
\(a=\displaystyle \frac{4}{5} \)
これは先ほど求めた \(0 \lt a \leqq 1\) を満たします。
よって、これが、 \(a=\displaystyle \frac{ソ}{タ} \) の答えになります。
もう \(1\) つの場合を計算してみましょう。
\(y=f(x)\) の最小値が \(f(p)\) のとき
\(f(p)\) は、頂点のときなので、先ほど平方完成した式を使いましょう。
\(f(x)=a\{x-\displaystyle \frac{(a+3)}{a}\}^2-\displaystyle \frac{(a+3)^2}{a}-3a+21\)
なので、
\(f(p)=-\displaystyle \frac{(a+3)^2}{a}-3a+21\)
これが最小値 \(1\) になるので、
\(-\displaystyle \frac{(a+3)^2}{a}-3a+21=1\)
この式を整理すると、
\(4a^2-14a+9=0\)
解の公式より、
\(a=\displaystyle \frac{7\pm\sqrt{13}}{4} \)
先ほど求めた \(1 \leqq a \) を満たすのは、\(a=\displaystyle \frac{7+\sqrt{13}}{4} \)
よって、これが、\(a=\displaystyle \frac{チ+\sqrt{ツテ}}{ト} \) の答えですね。
先の結果も合わせて
ソ=4、タ=5、チ=7、ツテ=13、ト=4
以上求まりました。