集合とは

集合の表し方

「1けたの奇数」のように、範囲がはっきりしたものの集まりを集合といいます。
集合を構成する $1$ つ $1$ つのものを要素といいます。

集合の表し方は、要素の満たす条件を書く方法と、要素を書き並べる方法があります。
例：「1けたの奇数全体の集合Ａ」
$Ａ=\{x | xは1けたの奇数\}$
$Ａ=\{1,3,5,7,9\}$

要素の個数が多い集合は、一部の要素を並べて、残りは・・・で表すこともあります。
例：「2けたの偶数全体の集合Ａ」
$Ａ=\{10,12,14,16,・・・,98\}$

要素の表し方

$a$ が集合 $A$ の要素であることを
$a \in A$ や $A \ni a$ で表します。
$b$ が集合 $A$ の要素でないことを
$b \notin A$ で表します。
例
$Ａ=\{x | 60の正の約数全体\}$
$5 \in A$
$40 \notin A$

部分集合・全体集合・空集合

部分集合

集合 $A$ と集合 $B$ について、$A$ のすべての要素が $B$ の要素でもあるとき、
$A$ は $B$ の部分集合であるといい、$A \subset B$
で表します。

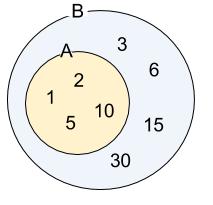
例１
$A=\{x | 10の正の約数全体\}$
$B=\{x | 30の正の約数全体\}$
のとき、$A \subset B$

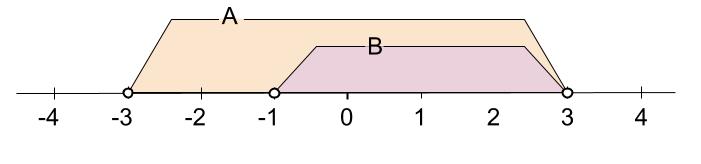
例２
$Ａ=\{x | -3 \lt x \lt 3\}$
$B=\{x | -1 \lt x \lt 3\}$
のとき、$B \subset A$

全体集合と空集合

部分集合の対になる言葉として、全体集合があります。
部分に対して、全体です。全体集合とは、要素の全体をあらわす集合です。
はっきり言って、この言葉にあまりこだわる必要はありません。
また、要素が $1$ つもない集合を空集合といい、$\phi$（ファイ）で表します。
空集合は、あらゆる集合の部分集合になります。

例題１

全体集合を $U=\{1,4,9\}$ とする。 $U$ の部分集合をすべてかきなさい。

解説

要素の個数が $0$ 個、$1$ 個、$2$ 個、$3$ 個と順にかき出していきます。
$\phi$
$\{1\}$、$\{4\}$、$\{9\}$
$\{1,4,\}$、$\{1,9\}$、$\{4,9\}$
$\{1,4,9\}$
以上、 $8$ つです。

$U$ 自身も $U$ の部分集合です。注意してください。
そして、空集合も部分集合です。
要素の数が $n$ 個の集合の部分集合は $2^n$ 個あります。
※数学Ａの場合の数の考え方でわかります。