2次関数

ko-su- 2次関数

グラフの平行移動　

２次関数の平行移動

前回、とても重要な「平行移動」について学習しました。

$y=f(x)$ のグラフを
$x$ 軸方向に $+p$
$y$ 軸方向に $+q$
平行移動すると、
$y-q=f(x-p)$ になる。

$2$ 次関数でいうと、
$y=ax^2$ のグラフを、
$x$ 軸方向に $+p$
$y$ 軸方向に $+q$
平行移動すると、
$y-q=a(x-p)^2$
になります。

いくつか具体例を見ていきましょう。

次の $2$ 次関数のグラフをかきなさい。
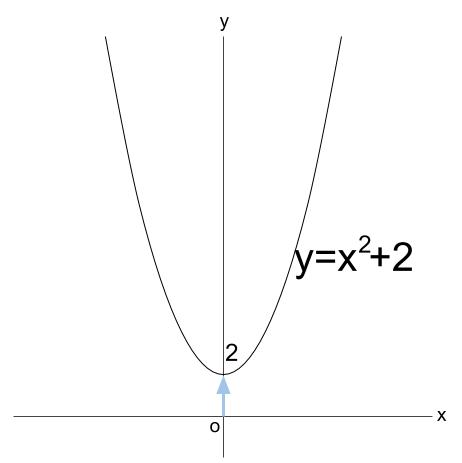
$y=x^2+2$

これは
$y-2=x^2$
のことですね。
もっと変形するならば
$y-2=(x-0)^2$
です。

つまり、
$y=x^2$ のグラフを
$y$ 軸方向に $+2$ 平行移動した放物線です。
※ $x$ 軸方向に $+0$ 平行移動した、とは $x$ 軸方向の移動はしていませんね。

$高校数学無料学習サイトko-su- 2次関数　y=x^2+2$

次の $2$ 次関数のグラフをかきなさい。
$y=-(x+3)^2$

これは
$y=-x^2$ のグラフを
$x$ 軸方向に $-3$ 平行移動した放物線です。
$y-q=a(x-p)^2$ の形に式変形することがポイントです。

$y=-(x+3)^2=-\{x-(-3)\}^2$

$y$ 軸方向の移動はしていませんね。

$x$ 軸方向の正、負、どちらの方向に移動したのか。
これに関わるのは、

$y=-(x$ $+$ $3)^2$ の赤字の符号のみです。
$y=-\{x$ $-$ $(-3)\}^2$

$y=$ $-$$(x+3)^2$ の青字の符号は、無関係です。
$y=$ $-$ $\{x-(-3)\}^2$
こちらの符号は、グラフが上に凸か下に凸かに関わる符号です。

$高校数学無料学習サイトko-su- 2次関数　y=-(x+3)^2$

次の $2$ 次関数のグラフをかきなさい。
$y=2(x-1)^2+4$

これは
$y-4=2(x-1)^2$
のことですね。

つまり、
$y=2x^2$ のグラフを
$x$ 軸方向に $+1$
$y$ 軸方向に $+4$ 平行移動した放物線です。

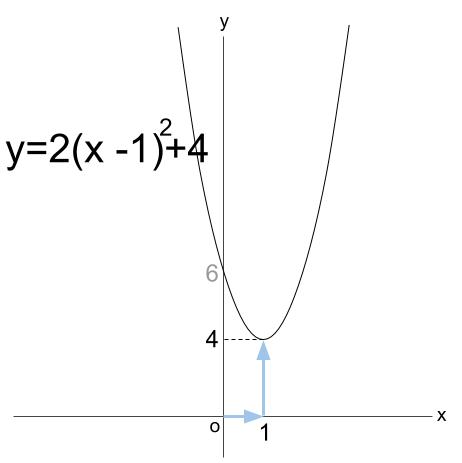
$高校数学無料学習サイトko-su- 2次関数　y=2(x-1)^2+4$

※図の比率は、不正確です。
厳密にかくと、$y=2x^2$ のグラフはかなり縦長になります。
フリーハンドで図示する場合、比率の正確さはあまり気にする必要はありません。