関数　\(y=f(x)\)

\(2\) 次関数という新しい関数を学習する前段階として、
「関数」の新しい表記を導入します。

一般に、 \(y\) が \(x\) の関数であることを \(f\) などの記号を使って、 \(y=f(x)\)
と表します。

また、関数 \(f(x)\) において、\(x\) に \(a\) を代入した値を \(f(a)\) で表します。

例
\(f(x)=x^2-2x+5\) において、\(f(-3)\) の値は、

\(f(-3)=(-3)^2-2×(-3)+5=20\)

\(y=f(x)\) という表記は、出てきたり出てこなかったりです。
あまり深く考えないで、見慣れてください。

\(2\) 次関数

\(2\) 次関数とはずばり、\(2\) 次式の関数です。

\(y=ax^2+bx+c\)
このような式で表されるものが \(2\) 次関数です。

中学では、\(y=ax^2\) を学習しました。

これは \(x\) の \(2\) 次関数の一部分を学習したということです。
\(b=c=0\) の特殊ケースのみを学習したのです。

ここからは、 \(2\) 次関数すべてを扱っていきます。

つまり、

\(y=3x^2-4x+1\)
とか
\(y=-5x^2+3\)
とか
\(y=x^2-x\)
などです。

\(x\) の \(1\) 次の項や、定数項のあるものたちです。

\(y=ax^2+bx+c\)
これが \(2\) 次関数です。
ただし、\(a \neq 0\) でないと \(2\) 次関数ではありません。

\(y=ax^2\) のグラフの概形

まずは中学数学の復習をしておきましょう。

\(y=ax^2\) のグラフは、
頂点は、原点 \(O\)
軸は \(y\) 軸です。
この曲線は、放物線ともよばれます。

\(y=ax^2\) のグラフの \(a \gt 0\)

下に凸（とつ）なグラフともいいます。

\(y=ax^2\) のグラフの \(a \lt 0\)

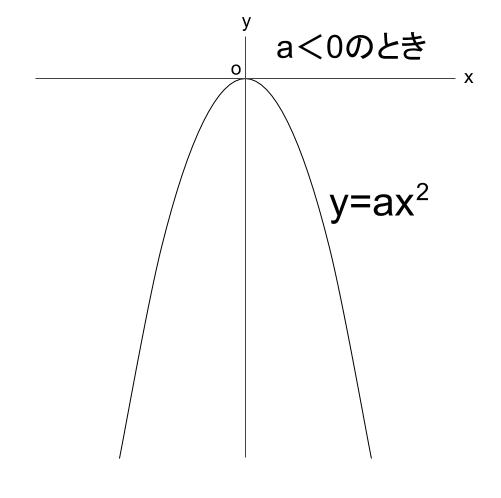
上に凸（とつ）なグラフともいいます。

グラフをかくときは、頂点と通る点（ \(1\) つか \(2\) つくらい）を曲線（放物線）で結びます。
フリーハンドで概形をかけばよいです。
精密にかくことはできませんし、それが求められることもまずありません。

グラフの概形と平行移動

一般の \(2\) 次関数のグラフがどのようになるのか、具体例を見てみましょう。

例
\(y=2x^2-12x+17\) のグラフの概形を例にします。

どのようなグラフになるのかは、
\(x=0\) のとき \(y=17\)
\(x=1\) のとき \(y=7\)
のように、無数の点をとって、それを結ぶことで得られます。

この作業は、みなさんはやらないでＯＫです。
やったらどうなるのか、という答えを教えてしまいます。

\(y=2x^2\) のグラフと同じ放物線になります。

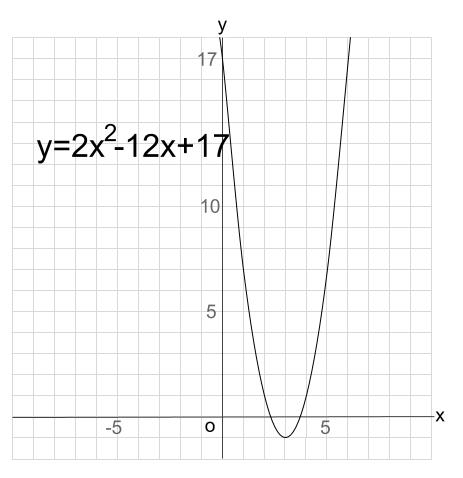
そうなんです、「同じ」なんです。
曲線の曲がり具合とか、同じなんです。

ただし、
座標平面上のどこに曲線があるか、が異なります。

\(1\)次関数でも似たようなものでしたね。
\(y=2x\)
と
\(y=2x+4\)
は、
直線そのものは同じで、座標平面上での位置だけが違いましたね。

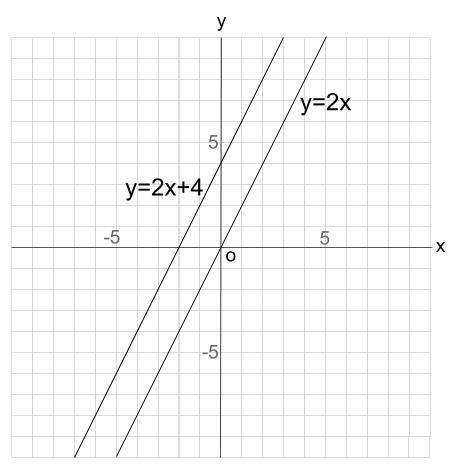
上で見たように、同じ曲線（グラフ）だけど、位置だけが違う。
これはグラフが座標平面の中を移動したように見なせます。
グラフがどれくらい移動したのかは
\(x\) 軸方向にいくつ
\(y\) 軸方向にいくつ
という \(2\) 方向で見ます。
それぞれ
\(x\) 軸方向の平行移動
\(y\) 軸方向の平行移動
といいます。

先の例でみると
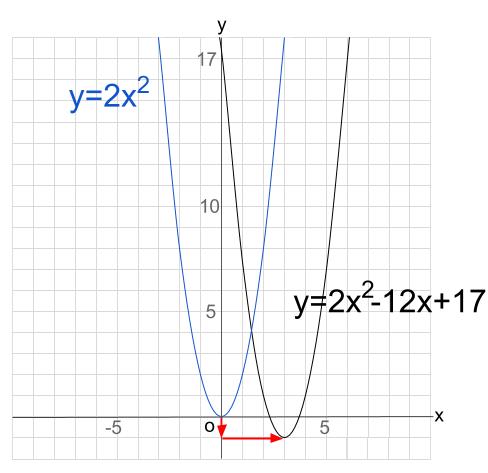
\(y=2x^2-12x+17\) のグラフは
\(y=2x^2\) を
\(x\) 軸方向に \(+3\)
\(y\) 軸方向に \(-1\)
平行移動させています。
グラフの頂点で読みとるのが楽ですね。

一般に、
\(y=ax^2\) と \(y=ax^2+bx+c\) は、まったく同じ曲線で、
座標平面上の位置だけが異なります。
\(x^2\) の係数 \(a\) が同じならば、同じ曲線です。
まずは覚えておきましょう。

平行移動の公式

さて、
\(y=2x^2-12x+17\) のグラフをかくとき、

毎度毎度、無数の点を取っていくのは面倒です。

\(y=2x^2\) を、どれだけ平行移動したのかさえ求まれば
グラフの概形をかくことができます。

つまり、
\(x\) 軸方向に \(+3\)
\(y\) 軸方向に \(-1\)
平行移動させれば、
\(y=2x^2-12x+17\)
になる、ということを
計算で求める方法が知りたいわけです。

ここで、\(y=f(x)\) のグラフの、平行移動の公式を示します。

\(y=f(x)\) のグラフの、平行移動の公式

これは、 \(2\) 次関数以外のあらゆる関数に成り立つことです。
今後も様々なところで出会うことになるでしょう。

なぜこれが成り立つのか。
いずれ時間に余裕ができれば別記事で書くこととします。
今は、あらゆる関数に成り立つ重要な性質として覚えてください。
そして、使いこなせるようになってください。

平行移動の具体例

\(y=2x^2\) を
\(x\) 軸方向に \(+3\)
\(y\) 軸方向に \(-1\)
平行移動させてみましょう。

上の公式の通りに式をかくと、
\(y-(-1)=2(x-3)^2\)

この式を変形していくと・・・
\(y+1=2(x^2-6x+9)\)
\(y+1=2x^2-12x+18\)
\(y=2x^2-12x+17\)

となり、確かに成り立っています。

つまり、
\(y=2x^2-12x+17\) のグラフをかきたいとき、
上で見た計算を逆にたどることで、
\(y=2x^2-12x+17\)
を
\(y-(-1)=2(x-3)^2\)
に式変形するわけです。

そうすれば、 \(y=2x^2\) を
\(x\) 軸方向に \(+3\)
\(y\) 軸方向に \(-1\)
平行移動させたグラフをかけばいい！！ということがわかります。

この計算方法の学習は、
次回からです。

\(2\) 次関数のグラフの学習を \(1\) つずつ進めていきましょう。