２次不等式・接点なし

2次不等式　共有点なし

$2$ 次関数のグラフが、 $x$ 軸と共有点を持たないときの $2$ 次不等式を見ていきましょう。

$2$ 次不等式は、必ず図示をして考えましょう。

次の $2$ 次不等式を解きなさい。

$x^2+3x+4 \geqq 0$

$y=x^2+3x+4$ のグラフをかきましょう。
グラフと $x$ 軸との位置関係や、共有点の座標が知りたいのです。

$x^2+3x+4=0$ を解くと、解がありません。
判別式
$D=3^2-4×1×4=-7 \lt 0$
からわかります。

よって、$y=x^2+3x+4$ のグラフは下図のようになります。

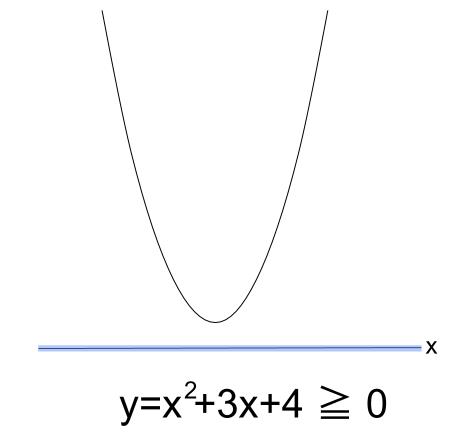
$高校数学無料学習サイトko-su- 2次不等式　ｘ軸との共有点なし1$

$y \geqq 0$ となる範囲が求める $x$ の範囲となります。

求める解は、「すべての実数」です。

$x^2+3x+4 \geqq 0$
$x^2+3x+4 \gt 0$
$x$ 軸との共有点がない場合、等号なのか、不等号なのか、の違いはありません。

どちらの $2$ 次不等式を解いても、上のようなグラフになり、
求める解は、「すべての実数」になります。

次の $2$ 次不等式を解きなさい。

$2x^2+4x+7 \leqq 0$

$2x^2+4x+7=0$ を解くと、解がありません。
判別式からわかります。

よって、$y=2x^2+4x+7$ のグラフは下図のようになります。

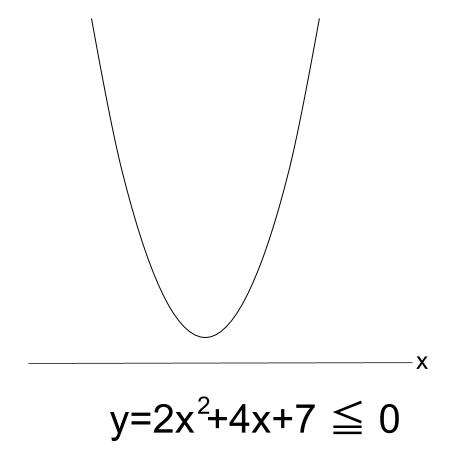
$高校数学無料学習サイトko-su- 2次不等式　ｘ軸との共有点なし2$

$y \leqq 0$ となる範囲が求める $x$ の範囲である。

求める解は、「なし」です。

$2x^2+4x+7 \leqq 0$
$2x^2+4x+7 \lt 0$
$x$ 軸との共有点がない場合、等号なのか、不等号なのか、の違いはありません。

どちらの $2$ 次不等式を解いても、上のようなグラフになり、
求める解は、「なし」になります。