三角方程式

数学Ⅰで学習した三角方程式と大差はありません。
角の範囲が $180°$ をこえただけです。
単位円による解法とグラフによる解法があります。

単位円による解法を断然おすすめします。

例題１

$0 \leqq \theta \lt 2\pi$ のとき、次の方程式を解きなさい。
$2\sin \theta+\sqrt{3}=0$

解説

等式を満たす $\theta$ を求めることが目標です。

$2\sin \theta+\sqrt{3}=0$ を変形して

$\sin \theta=-\displaystyle \frac{\sqrt{3}}{2}$

単位円で図示します。
$\sin \theta$ は単位円周上の $y$ 座標です。
結局、水色の直角三角形が有名三角形だから解けるのです。
$3$ 辺の比を覚えているから図示できるし、解けるのです。
そして、解ける問題しか出題されません。有名角のみが出題されるのです。

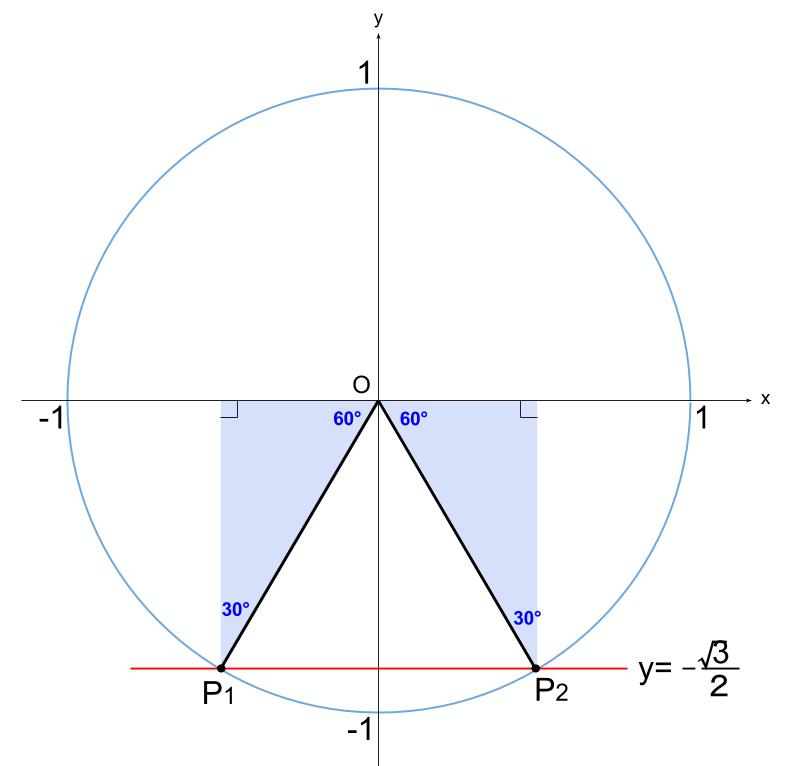
$OP_{1}$ と $OP_{2}$ の表す角が求める $\theta$ です。
$OP_{1}$ は $240°$
$OP_{2}$ は $300°$ ですね。
$0 \leqq \theta \lt 2\pi$ より、

$\theta=\displaystyle \frac{4}{3}\pi,\displaystyle \frac{5}{3}\pi$

別解

グラフでも解けます。

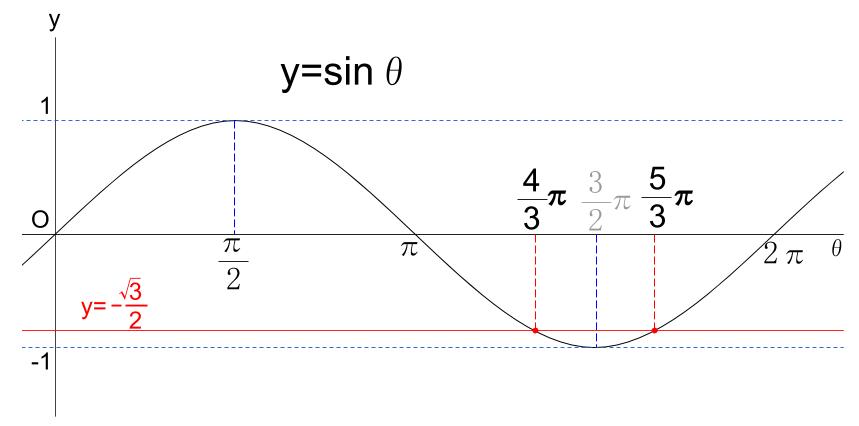
単位円による解法がおススメです。
グラフによる解法はおすすめはしません。

例題２

$0 \leqq \theta \lt 2\pi$ のとき、次の方程式を解きなさい。
$2\cos \theta= \sqrt{2}$

解説

等式を満たす $\theta$ を求めることが目標です。

$2\cos \theta= \sqrt{2}$ を変形して

$\cos \theta=\displaystyle \frac{\sqrt{2}}{2}$

単位円で図示します。
$\cos \theta$ は単位円周上の $x$ 座標です。
結局、水色の直角三角形が有名三角形だから解けるのです。
$3$ 辺の比を覚えているから図示できるし、解けるのです。

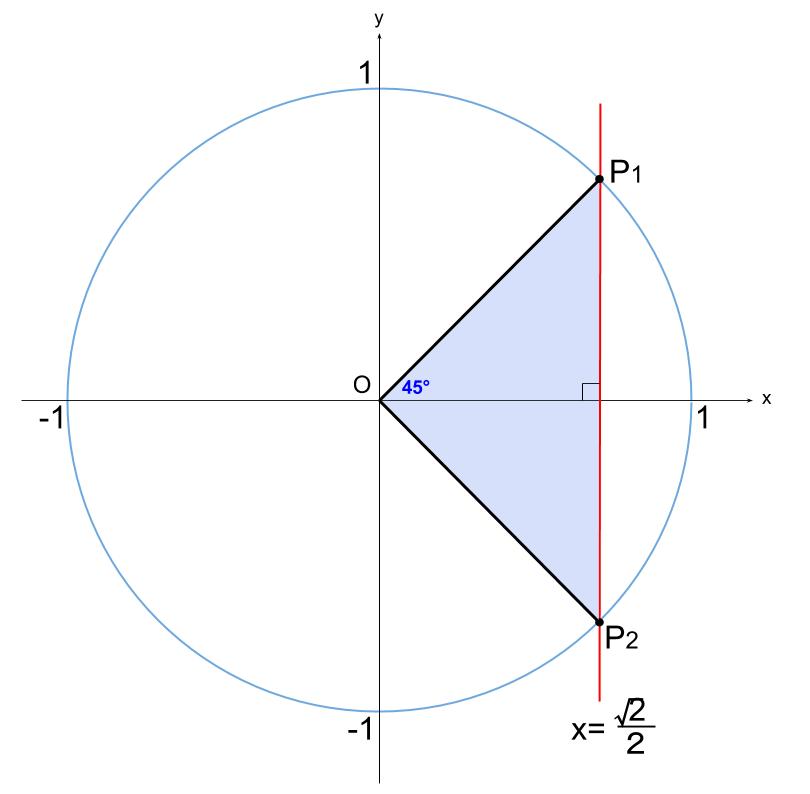
$OP_{1}$ と $OP_{2}$ の表す角が求める $\theta$ です。
$0 \leqq \theta \lt 2\pi$ より、

$\theta=\displaystyle \frac{\pi}{4},\displaystyle \frac{7}{4}\pi$

例題３

$0 \leqq \theta \lt 2\pi$ のとき、次の方程式を解きなさい。
$\tan \theta= -1$

解説

等式を満たす $\theta$ を求めることが目標です。

単位円で図示します。
$\tan \theta$ は直線の傾きです。
結局、水色の直角三角形が有名三角形だから解けるのです。
$3$ 辺の比を覚えているから図示できるし、解けるのです。

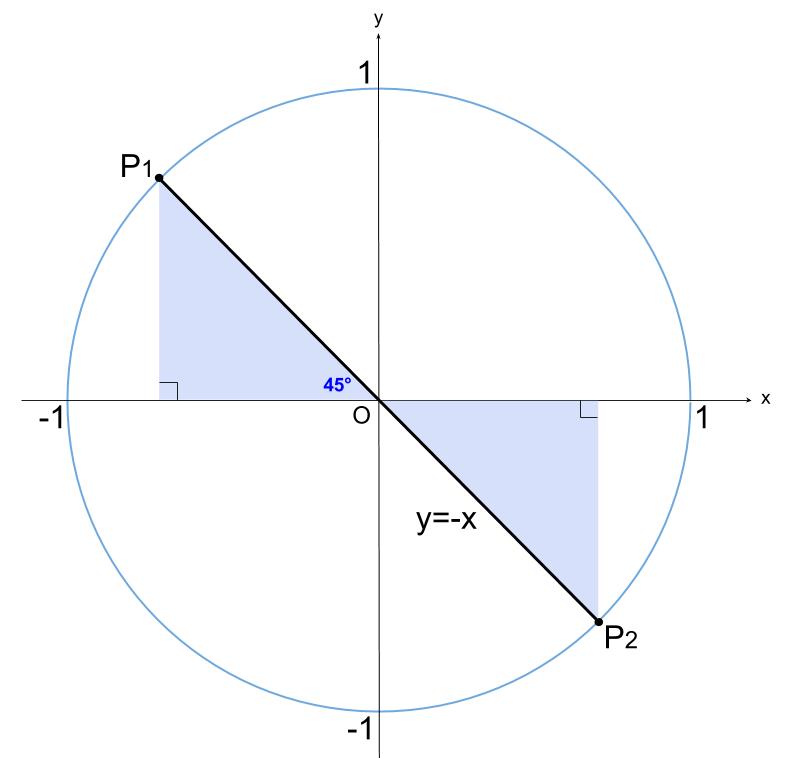
$OP_{1}$ と $OP_{2}$ の表す角が求める $\theta$ です。
$0 \leqq \theta \lt 2\pi$ より、

$\theta=\displaystyle \frac{3}{4}\pi,\displaystyle \frac{7}{4}\pi$