例題１

$0 \leqq \theta \lt 2\pi$ のとき、次の方程式 を解きなさい。
$\sin (2\theta-\displaystyle \frac{\pi}{4})=\displaystyle \frac{1}{2}$

解説

$2\theta-\displaystyle \frac{\pi}{4}= \alpha$ ・・・① とおくと、

$0 \leqq \theta \lt 2\pi$ のとき

$-\displaystyle \frac{\pi}{4} \leqq \alpha \lt \displaystyle \frac{15}{4} \pi$

※$\theta=0$、$\theta=2\pi$ を①に代入すればわかりますね。

これはつまり、$\theta=-\displaystyle \frac{\pi}{4}$ からスタートして、
反時計回りに $2$ 周する範囲ということです！！

赤が $1$ 周目
青が $2$ 周目

また、与式は
$\sin \alpha = \displaystyle \frac{1}{2}$

で、これを満たす $\alpha$ を求めることが目標です。

$\alpha =\displaystyle \frac{\pi}{6}+2n\pi , \displaystyle \frac{5}{6}\pi+2n\pi$ $(nは整数)$

が方程式を満たします。

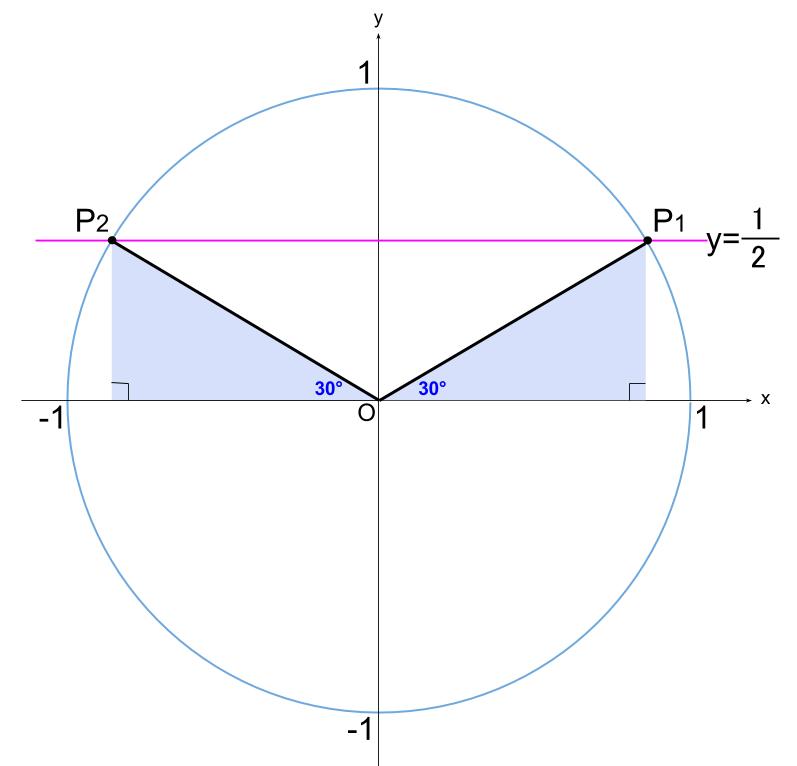
$-\displaystyle \frac{\pi}{4} \leqq \alpha \lt \displaystyle \frac{15}{4} \pi$ の範囲で

$\sin \alpha =\displaystyle \frac{1}{2}$ を解きます。

まず、１周目です。
下図より、
$\alpha =\displaystyle \frac{\pi}{6} ,\displaystyle \frac{5}{6}\pi$ がこの方程式を満たす解です。

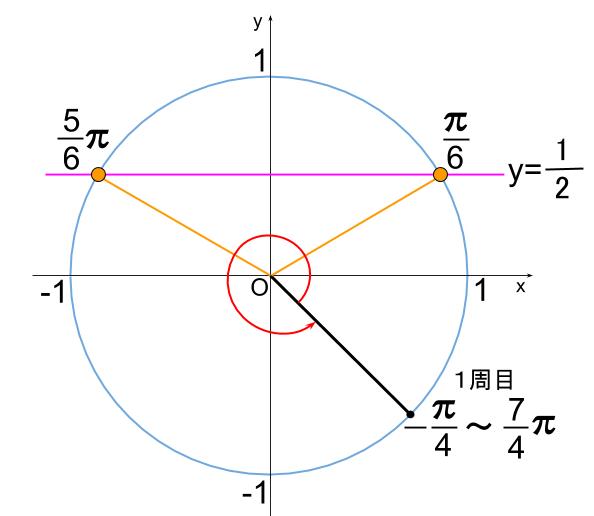
次に２周目です。
下図より、
$\alpha =\displaystyle \frac{13}{6}\pi ,\displaystyle \frac{17}{6}\pi$ がこの方程式を満たす解です。

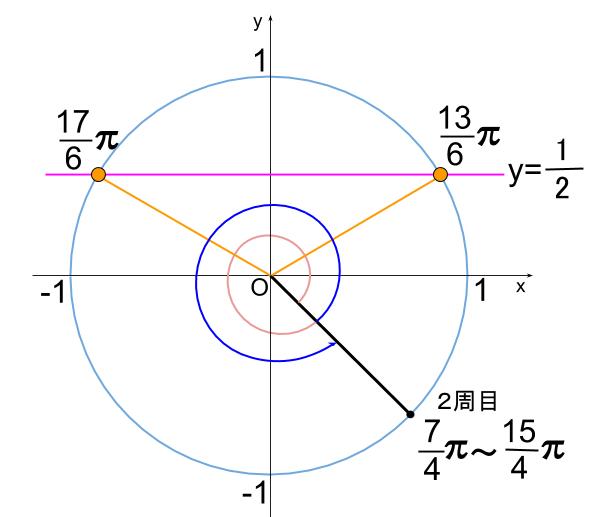
よって、
$\alpha =\displaystyle \frac{\pi}{6} ,\displaystyle \frac{5}{6}\pi , \displaystyle \frac{13}{6}\pi ,\displaystyle \frac{17}{6}\pi$
が解です。

最後に、$\alpha$ から $\theta$ にもどしましょう。

$2\theta-\displaystyle \frac{\pi}{4}= \alpha$ ・・・①
と最初におきましたね。

この式を $\theta$ について解きます。

$2\theta-\displaystyle \frac{\pi}{4}= \alpha$

$\theta-\displaystyle \frac{\pi}{8}= \displaystyle \frac{\alpha}{2}$

$\theta= \displaystyle \frac{\alpha}{2}+\displaystyle \frac{\pi}{8}$ ・・・③

これを使って$\alpha$ から $\theta$ にもどします。

$\alpha =\displaystyle \frac{\pi}{6} ,\displaystyle \frac{5}{6}\pi , \displaystyle \frac{13}{6}\pi ,\displaystyle \frac{17}{6}\pi$ をそれぞれ、③に代入します。

$\alpha =\displaystyle \frac{\pi}{6}$ を③に代入すると

$\theta= \displaystyle \frac{1}{2}×\displaystyle \frac{\pi}{6}+\displaystyle \frac{\pi}{8}=\displaystyle \frac{5}{24}\pi$

他 $3$ つも同様に③に代入して $\theta$ を求めます。
以下答えのみを記します。

$\theta= \displaystyle \frac{5}{24}\pi,\displaystyle \frac{13}{24}\pi,\displaystyle \frac{29}{24},\pi\displaystyle \frac{37}{24}\pi$

例題２

$0 \leqq \theta \lt 2\pi$ のとき、次の不等式 を解きなさい。
$\cos (2\theta+\displaystyle \frac{\pi}{3}) \leqq -\displaystyle \frac{\sqrt{3}}{2}$

解説

$2\theta+\displaystyle \frac{\pi}{3}= \alpha$ ・・・① とおくと、

$0 \leqq \theta \lt 2\pi$ のとき

$\displaystyle \frac{\pi}{3} \leqq \alpha \lt \displaystyle \frac{13}{3} \pi$

※$\theta=0$、$\theta=2\pi$ を代入した範囲

これはつまり、$\theta=\displaystyle \frac{\pi}{3}$ からスタートして、
反時計回りに $2$ 周する範囲ということです！！

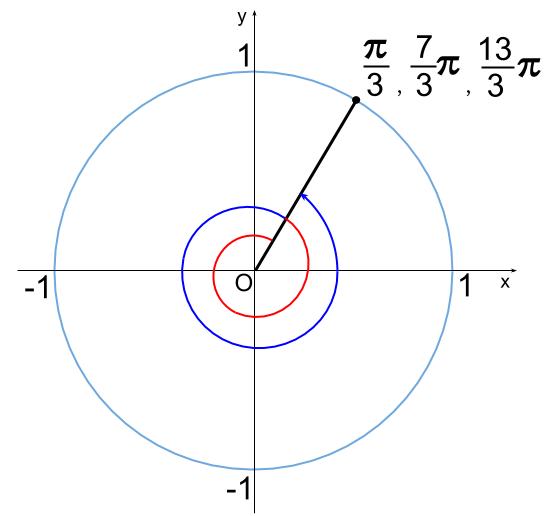
赤が $1$ 周目
青が $2$ 周目

また、与式は
$\cos \alpha \leqq -\displaystyle \frac{\sqrt{3}}{2}$

なので、

$\displaystyle \frac{5}{6}\pi+2n\pi \leqq \alpha \leqq \displaystyle \frac{7}{6} \pi+2n\pi$$(nは整数)$

が不等式を満たします。

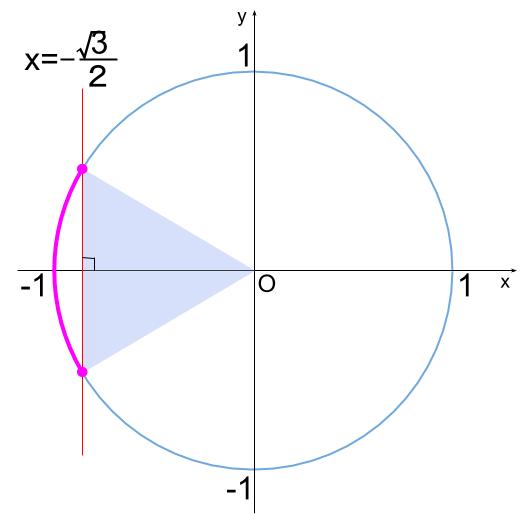
$\displaystyle \frac{\pi}{3} \leqq \alpha \lt \displaystyle \frac{13}{3} \pi$ の範囲で

$\cos \alpha \leqq -\displaystyle \frac{\sqrt{3}}{2}$ を解きます。

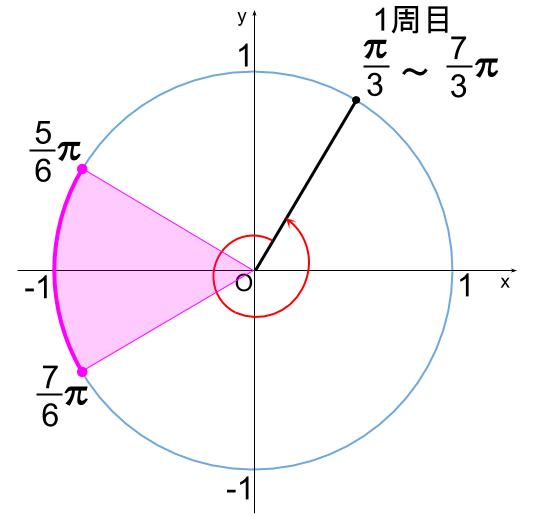
まず、１周目です。
下図より、
$\displaystyle \frac{5}{6}\pi \leqq \alpha \leqq \displaystyle \frac{7}{6}\pi$ がこの不等式を満たす解です。

次に２周目です。
下図より、
$\displaystyle \frac{17}{6}\pi \leqq \alpha \leqq \displaystyle \frac{19}{6}\pi$ がこの不等式を満たす解です。

よって、
$\displaystyle \frac{5}{6}\pi \leqq \alpha \leqq \displaystyle \frac{7}{6}\pi$、$\displaystyle \frac{17}{6}\pi \leqq \alpha \leqq \displaystyle \frac{19}{6}\pi$

が解です。

最後に、$\alpha$ から $\theta$ にもどしましょう。

$2\theta+\displaystyle \frac{\pi}{3}= \alpha$ ・・・①
と最初におきましたね。

この式を $\theta$ について解きます。

$2\theta+\displaystyle \frac{\pi}{3}= \alpha$

$\theta+\displaystyle \frac{\pi}{6}= \displaystyle \frac{\alpha}{2}$

$\theta= \displaystyle \frac{\alpha}{2}-\displaystyle \frac{\pi}{6}$ ・・・③

これを使って$\alpha$ から $\theta$ にもどします。

$\displaystyle \frac{5}{6}\pi \leqq \alpha \leqq \displaystyle \frac{7}{6}\pi$、$\displaystyle \frac{17}{6}\pi \leqq \alpha \leqq \displaystyle \frac{19}{6}\pi$ なので、

$\alpha=\displaystyle \frac{5}{6}\pi$ を③に代入して、$\theta= \displaystyle \frac{1}{4}\pi$

$\alpha=\displaystyle \frac{7}{6}\pi$ を③に代入して、$\theta= \displaystyle \frac{5}{12}\pi$
より、
$\displaystyle \frac{1}{4}\pi \leqq \theta \leqq \displaystyle \frac{5}{12}\pi$

同様に、$\displaystyle \frac{17}{6}\pi \leqq \alpha \leqq \displaystyle \frac{19}{6}\pi$ からは

$\displaystyle \frac{5}{4}\pi \leqq \theta \leqq \displaystyle \frac{17}{12}\pi$