複素数と高次方程式

ko-su- 複素数と高次方程式

１の３乗根

１の３乗根 $\omega$ （オメガ）

$1$ の $3$ 乗根とは、 $3$ 乗して $1$ になる数のことであり、つまり

$x^3=1$

という $3$ 次方程式の解です。

この方程式の解は $3$ つあります。

$1$ と $\displaystyle \frac{-1 \pm \sqrt{3}i}{2}$ です。

虚数の解が $2$ つありますが、そのうちの $1$ つを $\omega$ （オメガと読む）とすると、
以下のことが成り立ちます。

$\omega^3=1$

$\omega^2$ も$1$ の $3$ 乗根
※ちなみに、$\omega^2$ は、$\omega$ としなかったもう $1$ つの虚数解です。

つまり、$1$ の $3$ 乗根は、$1$ と $\omega$ と $\omega^2$ の $3$ つ。

この $3$ つの和は $0$ になります。
$\omega^2+\omega+1=0$

上の性質は、$2$ つの虚数解の、どちらを $\omega$ としても成り立ちます。
※数学Ⅲで、複素数平面を学習することでいろいろ納得されると思います。

以上のことから成り立つ性質として、以下のことが重要です。

$k$ を自然数とすると

$\omega^{3k}=(\omega^3)^k=1^k=1$

$\omega^{3k+1}=\omega^{3k} \cdot \omega=\omega$

$\omega^{3k+2}=\omega^{3k} \cdot \omega^2=\omega^2$

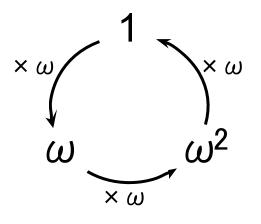
$高校数学無料学習サイトko-su- オメガの輪環の順$
この性質を用いて、$\omega^k$ の次数を下げることができます。

例えば
$\omega^{100}=\omega^{99} \cdot \omega=(\omega^3)^{33} \cdot \omega=\omega$

例題１

$x^3=1$ の虚数解の $1$ つを $\omega$ とするとき、次の式の値を求めなさい。

（１）$\omega^{10}+\omega^8$
（２）$(1+\omega-\omega^2)(1-\omega+\omega^2)$
（３）$(1+\omega)(1+\omega^2)(1-\omega^4)(1-\omega^5)$

解説

（１）$\omega^{10}+\omega^8$

$\omega^3=1$ なので、
$\omega^{10}=\omega^9 \cdot \omega=(\omega^3)^3 \cdot \omega=\omega$

$\omega^8=\omega^6 \cdot \omega^2=(\omega^3)^2 \cdot \omega^2=\omega^2$

したがって、
$\omega^{10}+\omega^8=\omega+\omega^2$

$=(\omega^2+\omega+1)-1$

$=-1$

※ $\omega^2+\omega+1=0$ を用いました。

（２）$(1+\omega-\omega^2)(1-\omega+\omega^2)$

$\omega^2+\omega+1=0$ なので、 $\omega^2=-\omega-1$
これを与式に代入すると、

$(1+\omega-\omega^2)(1-\omega+\omega^2)$

$=\{1+\omega-(-\omega-1)\}\{1-\omega+(-\omega-1)\}$

$=(1+\omega+\omega+1)(1-\omega-\omega-1)$

$=2(1+\omega)(-2\omega)$

$=-4(\omega+\omega^2)$

$=-4(\omega+\omega^2+1-1)$

$=-4×(-1)$

$=4$

（３）$(1+\omega)(1+\omega^2)(1-\omega^4)(1-\omega^5)$

$(1+\omega)(1+\omega^2)(1-\omega^4)(1-\omega^5)$

$=(1+\omega)(1+\omega^2)(1-\omega^3\cdot \omega)(1-\omega^3\cdot \omega^2)$

$=(1+\omega)(1+\omega^2)(1-\omega)(1-\omega^2)$

$=(1+\omega)(1-\omega)×(1+\omega^2)(1-\omega^2)$

$=(1-\omega^2)(1-\omega^4)$

$=(1-\omega^2)(1-\omega)$

$=(1-\omega-\omega^2+\omega^3)$

$=(1-\omega-\omega^2+1)$

$=(2-\omega-\omega^2)$

$=\{2-(\omega+\omega^2)\}$

$=\{2-(-1)\}$

$=3$

オメガに関する考察

オメガの値

方程式、$x^3=1$ を解いてみましょう。

$x^3=1$
$x^3-1=0$
因数分解の公式を適用して、
$(x-1)(x^2+x+1)=0$
したがって、
$x-1=0$ または、
$x^2+x+1=0$

$x-1=0$ のとき、 $x=1$
$x^2+x+1=0$ のとき、
$x^2+x+1=0$ に解の公式を用いて、
$x=\displaystyle \frac{-1 \pm \sqrt{1^2-4\cdot1\cdot1}}{2}$

$\displaystyle \frac{-1 \pm \sqrt{3}i}{2}$

以上より、$x^3=1$ を満たす $x$ は

$1,\displaystyle \frac{-1 \pm \sqrt{3}i}{2}$ です。

オメガの公式の確認

虚数の解が $2$ つありますが、そのうちの $1$ つを $\omega$ とすると、

$\omega^2$ も$1$ の $3$ 乗根
※ちなみに、$\omega^2$ は、$\omega$ としなかったもう $1$ つの虚数解です。

$\omega^2+\omega+1=0$

が成り立ちます。

これらが確かに成り立つことを確かめておきましょう。

$\omega^2$ も$1$ の $3$ 乗根

結局 $\omega$ は $\displaystyle \frac{-1 +\sqrt{3}i}{2}$ でも、$\displaystyle \frac{-1 -\sqrt{3}i}{2}$ でも、どちらでも良いということなのですが・・・

確かめておきましょう。

$\omega=\displaystyle \frac{-1 +\sqrt{3}i}{2}$ とすると、

$\omega^2=(\displaystyle \frac{-1 +\sqrt{3}i}{2})^2$

$= \displaystyle \frac{1 -2\sqrt{3}i-3}{4}$

$= \displaystyle \frac{-2 -2\sqrt{3}i}{4}$

$= \displaystyle \frac{-1 -\sqrt{3}i}{2}$

確かに、$\omega^2$ は、$\omega$ としなかったもう $1$ つの虚数解です。

では、
$\omega=\displaystyle \frac{-1 -\sqrt{3}i}{2}$ とすると、

$\omega^2=(\displaystyle \frac{-1 -\sqrt{3}i}{2})^2$

$= \displaystyle \frac{1 +2\sqrt{3}i-3}{4}$

$= \displaystyle \frac{-2 +2\sqrt{3}i}{4}$

$= \displaystyle \frac{-1 +\sqrt{3}i}{2}$

こちらも、$\omega^2$ は、$\omega$ としなかったもう $1$ つの虚数解です。

$\omega^2+\omega+1=0$

実際に計算して見るとすぐにわかります。

$\displaystyle \frac{-1 +\sqrt{3}i}{2}+\displaystyle \frac{-1 -\sqrt{3}i}{2}+1=0$

カテゴリー: 複素数と高次方程式

高校数学の無料オンライン学習サイトko-su-

１の３乗根

１の３乗根 \(\omega\) （オメガ）

例題１

解説

（１）\(\omega^{10}+\omega^8\)

（２）\((1+\omega-\omega^2)(1-\omega+\omega^2)\)

（３）\((1+\omega)(1+\omega^2)(1-\omega^4)(1-\omega^5)\)

オメガに関する考察

オメガの値

オメガの公式の確認

\(\omega^2\) も\(1\) の \(3\) 乗根

\(\omega^2+\omega+1=0\)